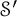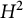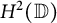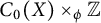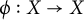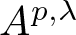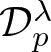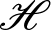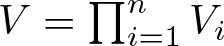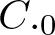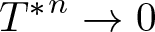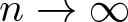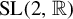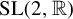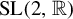Refine listing
Actions for selected content:
321 results in 47Bxx
Isometric dilation and Sarason’s commutant lifting theorem in several variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 25 February 2025, pp. 1-33
-
- Article
- Export citation
On commutators of square-zero Hilbert space operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-36
-
- Article
- Export citation
The algebraic numerical range as a spectral set in Banach algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extending surjective maps preserving the norm of symmetric Kubo-Ando means
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 777-786
- Print publication:
- September 2025
-
- Article
- Export citation
Cyclicity of the shift operator through Bezout identities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 January 2025, pp. 684-708
- Print publication:
- September 2025
-
- Article
- Export citation
On several dynamical properties of shifts acting on directed trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-30
-
- Article
- Export citation
New aspects of Bargmann transform using Touchard polynomials and hypergeometric functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-46
-
- Article
- Export citation
On spectra of Hankel operators on the polydisc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 301-317
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Beurling type invariant subspaces on Hardy and Bergman spaces of the unit ball or polydisk
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 232-245
- Print publication:
- March 2025
-
- Article
- Export citation
Embedding of some classes of operators into strongly continuous semigroups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 219-231
- Print publication:
- March 2025
-
- Article
- Export citation
Nearly invariant Brangesian subspaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 318-337
- Print publication:
- March 2025
-
- Article
- Export citation
Compact elements and the hypocompact radical of crossed products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 349-358
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Localization in the random XXZ quantum spin chain
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 03 January 2025, e129
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a class of bivariate distributions built of q-ultraspherical polynomials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-34
-
- Article
- Export citation
Hilbert type operators acting from the Bloch space into Bergman spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 205-225
-
- Article
- Export citation
Cesàro-type operators on Bergman–Morrey spaces and Dirichlet–Morrey spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 268-299
-
- Article
- Export citation
Minimal isometric dilations and operator models for the polydisc
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-40
-
- Article
- Export citation
Compact bilinear operators and paraproducts revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 44-59
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniformity aspects of
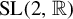 ${\mathrm {SL}}(2,{\mathbb R})$ cocycles and applications to Schrödinger operators defined over Boshernitzan subshifts
${\mathrm {SL}}(2,{\mathbb R})$ cocycles and applications to Schrödinger operators defined over Boshernitzan subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1734-1756
- Print publication:
- June 2025
-
- Article
- Export citation
Maximal noncompactness of limiting Sobolev embeddings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-19
-
- Article
- Export citation



 . When
. When 
 and its norm-closure
and its norm-closure  . In the infinite-dimensional setting, we characterise the intersection of
. In the infinite-dimensional setting, we characterise the intersection of  with the set of biquasitriangular operators, and we exhibit an index obstruction to belonging to
with the set of biquasitriangular operators, and we exhibit an index obstruction to belonging to  .
.