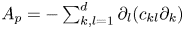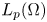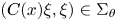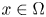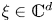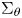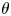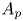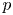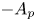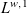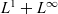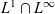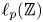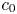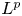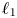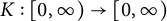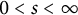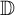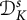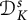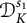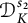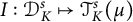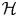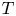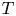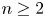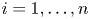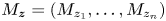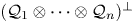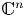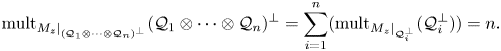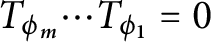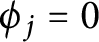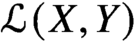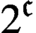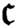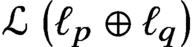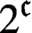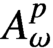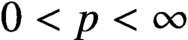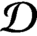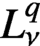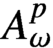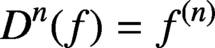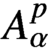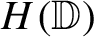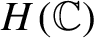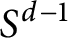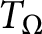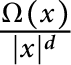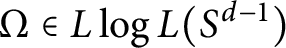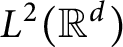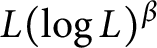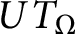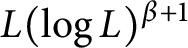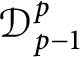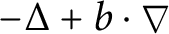Refine listing
Actions for selected content:
321 results in 47Bxx
On sectoriality of degenerate elliptic operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 18 August 2021, pp. 689-710
-
- Article
- Export citation
EXTREME POINT METHODS IN THE STUDY OF ISOMETRIES ON CERTAIN NONCOMMUTATIVE SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 06 August 2021, pp. 462-483
- Print publication:
- May 2022
-
- Article
- Export citation
THE RESOLVENT AND RIESZ TRANSFORM ON CONNECTED SUMS OF MANIFOLDS WITH DIFFERENT ASYMPTOTIC DIMENSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 24 June 2021, pp. 344-345
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
Chaos and frequent hypercyclicity for composition operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 513-531
-
- Article
- Export citation
Characterizations of Morrey type spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 328-344
- Print publication:
- June 2022
-
- Article
- Export citation
Multiplicities, invariant subspaces and an additive formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 279-297
-
- Article
- Export citation
AN UNBOUNDED OPERATOR WITH SPECTRUM IN A STRIP AND MATRIX DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 16 April 2021, pp. 146-153
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
Cantor spectrum for CMV and Jacobi matrices with coefficients arising from generalized skew-shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2009-2027
- Print publication:
- June 2022
-
- Article
- Export citation
Zero products of Toeplitz operators on Reinhardt domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 170-179
- Print publication:
- March 2022
-
- Article
- Export citation
Banach spaces for which the space of operators has 2𝔠 closed ideals
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 19 March 2021, e27
-
- Article
-
- You have access
- Open access
- Export citation
Characterizations of Hankel operators in the essential commutant of quasicontinuous Toeplitz operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 44-51
- Print publication:
- March 2022
-
- Article
- Export citation
GENERALISED WEIGHTED COMPOSITION OPERATORS ON BERGMAN SPACES INDUCED BY DOUBLING WEIGHTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 141-153
- Print publication:
- August 2021
-
- Article
- Export citation
Chaos and frequent hypercyclicity for weighted shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 28 December 2020, pp. 3634-3670
- Print publication:
- December 2021
-
- Article
- Export citation
WEIGHTED COMPOSITION OPERATORS BETWEEN LORENTZ SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 493-505
- Print publication:
- June 2021
-
- Article
- Export citation
Inequalities on partial traces of positive semidefinite block matrices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 964-969
- Print publication:
- December 2021
-
- Article
- Export citation
An estimate for the composition of rough singular integral operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 07 December 2020, pp. 911-922
- Print publication:
- December 2021
-
- Article
- Export citation
Lattice isomorphisms between projection lattices of von Neumann algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e49
-
- Article
-
- You have access
- Open access
- Export citation
Embedding of Dirichlet type spaces
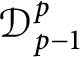 $\mathcal {D}^{p}_{p-1 }$ into tent spaces and Volterra operators
$\mathcal {D}^{p}_{p-1 }$ into tent spaces and Volterra operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 September 2020, pp. 697-708
- Print publication:
- September 2021
-
- Article
- Export citation
Regularity theory of Kolmogorov operator revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 24 August 2020, pp. 725-736
- Print publication:
- December 2021
-
- Article
- Export citation
VARIANTS OF ANDO–HIAI TYPE INEQUALITIES FOR DEFORMED MEANS AND APPLICATIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 17 August 2020, pp. 622-639
- Print publication:
- September 2021
-
- Article
- Export citation