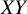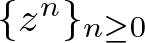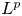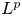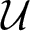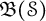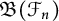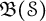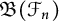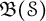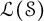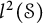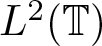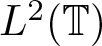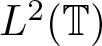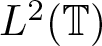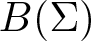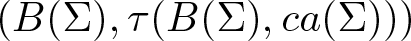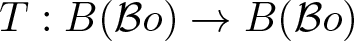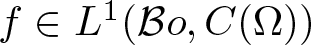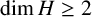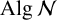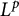Refine listing
Actions for selected content:
321 results in 47Bxx
A note on the space of all Toeplitz operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 November 2024, pp. 1123-1140
- Print publication:
- December 2024
-
- Article
- Export citation
Inhomogeneous isotropic quantum spin chain associated with the difference Lamé equation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A class of Hausdorff–Berezin operators on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 23 October 2024, pp. 1069-1080
- Print publication:
- December 2024
-
- Article
- Export citation
 $L^p$-BOUNDEDNESS OF THE BEREZIN TRANSFORM ON GENERALISED HARTOGS TRIANGLES
$L^p$-BOUNDEDNESS OF THE BEREZIN TRANSFORM ON GENERALISED HARTOGS TRIANGLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 541-551
- Print publication:
- June 2025
-
- Article
- Export citation
Solid bases and functorial constructions for (p-)Banach spaces of analytic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 09 September 2024, pp. 1013-1044
-
- Article
- Export citation
Lp positivity preservation and self-adjointness of Schrödinger operators on incomplete Riemannian manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterization of continuous homomorphisms on entire slice monogenic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 17 May 2024, pp. 892-920
-
- Article
- Export citation
A reproducing kernel approach to Lebesgue decomposition
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1570-1610
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Growth of hypercyclic functions: a continuous path between
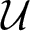 $\mathcal{U}$-frequent hypercyclicity and hypercyclicity
$\mathcal{U}$-frequent hypercyclicity and hypercyclicity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 08 May 2024, pp. 794-829
-
- Article
- Export citation
Dirichlet-type spaces of the unit bidisc and toral 2-isometries
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1271-1293
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Range inclusion and diagonalization of complex symmetric operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 04 April 2024, pp. 1222-1242
- Print publication:
- August 2025
-
- Article
- Export citation
Thompson’s semigroup and the first Hochschild cohomology
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 842-862
- Print publication:
- June 2025
-
- Article
- Export citation
Nonexpansive and noncontractive mappings on the set of quantum pure states
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1366-1384
- Print publication:
- August 2025
-
- Article
- Export citation
Commutants and complex symmetry of finite Blaschke product multiplication operator in
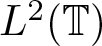 $L^2(\mathbb{T})$
$L^2(\mathbb{T})$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 261-286
-
- Article
- Export citation
On traces of Bochner representable operators on the space of bounded measurable functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 224-235
-
- Article
- Export citation
The lower bounds of non-real eigenvalues for singular indefinite Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1051-1060
- Print publication:
- June 2025
-
- Article
- Export citation
2-LOCAL ISOMETRIES OF SOME NEST ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 367-376
- Print publication:
- October 2024
-
- Article
- Export citation
Extension of monotone operators and Lipschitz maps invariant for a group of isometries
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 December 2023, pp. 149-186
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear fractional self-maps of the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 November 2023, pp. 458-468
- Print publication:
- June 2024
-
- Article
- Export citation
ISOMETRIES AND HERMITIAN OPERATORS ON SPACES OF VECTOR-VALUED LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 1857-1874
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation