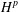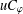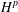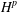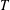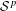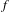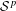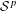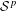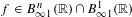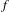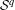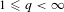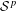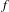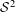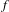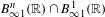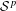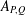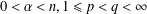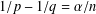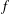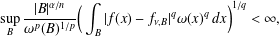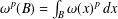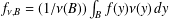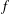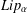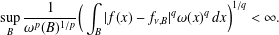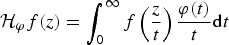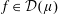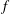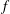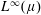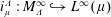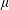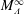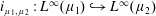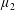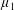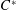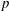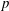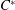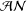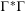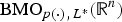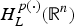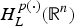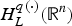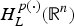Refine listing
Actions for selected content:
321 results in 47Bxx
COMPACT WEIGHTED COMPOSITION OPERATORS ON
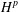 $H^{p}$-SPACES
$H^{p}$-SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 26 February 2019, pp. 473-484
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
APPROXIMATELY ANGLE PRESERVING MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 14 February 2019, pp. 485-496
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
HIGHER ORDER DIFFERENTIABILITY OF OPERATOR FUNCTIONS IN SCHATTEN NORMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 13 February 2019, pp. 1993-2016
- Print publication:
- November 2020
-
- Article
- Export citation
CHARACTERIZATIONS OF BMO AND LIPSCHITZ SPACES IN TERMS OF
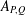 $A_{P,Q}$ WEIGHTS AND THEIR APPLICATIONS
$A_{P,Q}$ WEIGHTS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 381-391
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Hausdorff operators on holomorphic Hardy spaces and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1095-1112
- Print publication:
- June 2020
-
- Article
- Export citation
Estimates for the order of Nevanlinna matrices and a Berezanskii-type theorem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1637-1661
- Print publication:
- December 2019
-
- Article
- Export citation
Cyclicity in Dirichlet Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 247-257
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Embeddings of Müntz Spaces in
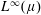 $L^{\infty }(\unicode[STIX]{x1D707})$
$L^{\infty }(\unicode[STIX]{x1D707})$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1-9
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Maps on Quantum States in
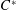 $C^{\ast }$-algebras Preserving von Neumann Entropy or Schatten
$C^{\ast }$-algebras Preserving von Neumann Entropy or Schatten 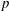 $p$-norm of Convex Combinations
$p$-norm of Convex Combinations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 75-80
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Commuting and Semi-commuting Monomial-type Toeplitz Operators on Some Weakly Pseudoconvex Domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 327-340
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Linear Maps Preserving Matrices of Local Spectral Radius Zero at a Fixed Vector
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 749-771
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
A NOTE ON POSITIVE
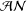 ${\mathcal{A}}{\mathcal{N}}$ OPERATORS
${\mathcal{A}}{\mathcal{N}}$ OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 129-130
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
INVERSION OF OPERATOR PENCILS ON HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 145-176
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
SPECTRA OF LINEAR FRACTIONAL COMPOSITION OPERATORS ON THE GROWTH SPACE AND BLOCH SPACE OF THE UPPER HALF-PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 199-214
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
INVERSE SPECTRAL THEORY FOR A CLASS OF NON-COMPACT HANKEL OPERATORS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 06 September 2018, pp. 132-156
- Print publication:
- 2019
-
- Article
- Export citation
FOURIER-TYPE TRANSFORMS ON REARRANGEMENT-INVARIANT QUASI-BANACH FUNCTION SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 231-248
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
FREQUENTLY HYPERCYCLIC BILATERAL SHIFTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 271-286
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
On Universal Operators and Universal Pairs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 08 June 2018, pp. 891-908
-
- Article
- Export citation
Variable Hardy Spaces Associated with Operators Satisfying Davies–Gaffney Estimates
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 759-810
-
- Article
- Export citation
The Fréchet Schwartz Algebra of Uniformly Convergent Dirichlet Series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 07 May 2018, pp. 933-942
-
- Article
- Export citation