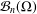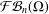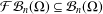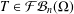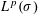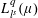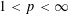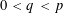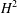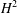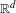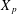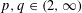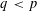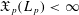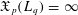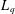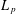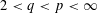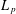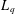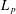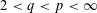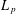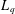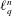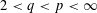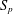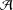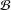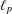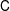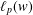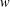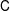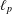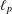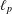Refine listing
Actions for selected content:
321 results in 47Bxx
THE STRONG IRREDUCIBILITY OF A CLASS OF COWEN–DOUGLAS OPERATORS ON BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 479-488
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
CONTINUITY OF THE HAUSDORFF DIMENSION FOR GRAPH-DIRECTED SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 471-478
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
TWO-WEIGHT NORM INEQUALITIES FOR VECTOR-VALUED OPERATORS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 July 2016, pp. 72-91
- Print publication:
- 2017
-
- Article
- Export citation
‘POSITIVELY HOMOGENEOUS LATTICE HOMOMORPHISMS BETWEEN RIESZ SPACES NEED NOT BE LINEAR’
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 444-445
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
A SPECTRAL CHARACTERIZATION OF
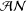 ${\mathcal{A}}{\mathcal{N}}$ OPERATORS
${\mathcal{A}}{\mathcal{N}}$ OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 369-391
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
THE CESÀRO OPERATOR IN THE FRÉCHET SPACES ℓp+ AND L p−
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 273-287
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
Coincidence Results for Summing Multilinear Mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 03 June 2016, pp. 877-897
-
- Article
- Export citation
SPLITTING INVARIANT SUBSPACES IN THE HARDY SPACE OVER THE BIDISK
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 12 May 2016, pp. 205-223
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
LOCAL DECAY FOR THE DAMPED WAVE EQUATION IN THE ENERGY SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 01 April 2016, pp. 509-540
- Print publication:
- June 2018
-
- Article
- Export citation
SEMIGROUPS OF COMPOSITION OPERATORS ON LOCAL DIRICHLET SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 144-154
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
METRIC
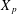 $X_{p}$ INEQUALITIES
$X_{p}$ INEQUALITIES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 4 / 2016
- Published online by Cambridge University Press:
- 02 February 2016, e3
-
- Article
-
- You have access
- Open access
- Export citation
A LIMITING CASE OF ULTRASYMMETRIC SPACES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 929-948
- Print publication:
- 2016
-
- Article
- Export citation
Orthogonally Additive Polynomials and Orthosymmetric Maps in Banach Algebras with Properties 𝔸 and 𝔹
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 15 December 2015, pp. 559-568
-
- Article
- Export citation
The Weyl–von Neumann theorem and Borel complexity of unitary equivalence modulo compacts of self-adjoint operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 29 October 2015, pp. 1115-1144
- Print publication:
- December 2015
-
- Article
- Export citation
A CHARACTERISATION OF 3-JORDAN HOMOMORPHISMS ON BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 04 September 2015, pp. 301-306
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
SPECTRUM AND COMPACTNESS OF THE CESÀRO OPERATOR ON WEIGHTED
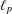 $\ell _{p}$ SPACES
$\ell _{p}$ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 287-314
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
STABILITY OF UNCONDITIONAL SCHAUDER DECOMPOSITIONS IN
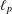 $\ell _{p}$ SPACES
$\ell _{p}$ SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 03 August 2015, pp. 444-456
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
UNIFORMLY BOUNDED COMPOSITION OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 463-469
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
CLASSES OF SEQUENTIALLY LIMITED OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 22 July 2015, pp. 573-586
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
EMBEDDING AND TRACE RESULTS FOR VARIABLE EXPONENT SOBOLEV AND MAZ'YA SPACES ON NON-SMOOTH DOMAINS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 471-489
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation