Refine listing
Actions for selected content:
321 results in 47Bxx
Discrete Tracy–Widom operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 545-559
-
- Article
-
- You have access
- Export citation
n-JORDAN HOMOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 19 June 2009, pp. 159-164
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
BELLWETHERS FOR BOUNDEDNESS OF COMPOSITION OPERATORS ON WEIGHTED BANACH SPACES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 01 June 2009, pp. 305-314
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
THE ESSENTIAL NORM OF A WEIGHTED COMPOSITION OPERATOR FROM THE BLOCH SPACE TO H∞
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 05 May 2009, pp. 487-497
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
DIFFERENCES OF COMPOSITION OPERATORS ON THE BLOCH SPACE IN THE POLYDISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 465-471
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
COMPACT LEFT MULTIPLIERS ON BANACH ALGEBRAS RELATED TO LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 227-238
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
A KADISON–SAKAI-TYPE THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 249-257
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
ISOMETRIES AND SPECTRA OF MULTIPLICATION OPERATORS ON THE BLOCH SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 147-160
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
THE FINITE SUM OF THE PRODUCTS OF TWO TOEPLITZ OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 45-60
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
Composition operators on μ-Bloch spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 50-75
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
Bounded Hankel Products on the Bergman Space of the Polydisk
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 190-204
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
FUNCTIONAL CALCULUS EXTENSIONS ON DUAL SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 10 March 2009, pp. 71-77
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
p-VARIATION OF VECTOR MEASURES WITH RESPECT TO BILINEAR MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 411-430
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
CONTINUITY OF WEIGHTED COMPOSITION OPERATORS BETWEEN WEIGHTED BLOCH TYPE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 111-115
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
CONVOLUTION OPERATORS AND HOMOMORPHISMS OF LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 329-344
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
THE SPECTRAL TYPE OF SUMS OF OPERATORS ON NON-HILBERTIAN BANACH LATTICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 193-198
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
DIFFERENCES OF COMPOSITION OPERATORS BETWEEN WEIGHTED BANACH SPACES OF HOLOMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 9-20
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
LOCAL PROPERTIES OF THE HOCHSCHILD COHOMOLOGY OF C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 117-130
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
COMPACT DIFFERENCES OF COMPOSITION OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 161-165
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Weighted composition operators on Orlicz-Sobolev spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-334
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
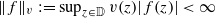 . We call
. We call 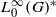 for a locally compact group
for a locally compact group 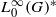 , and prove that the existence of a compact left multiplier on
, and prove that the existence of a compact left multiplier on 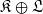 and
and 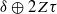 , where
, where 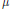
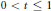
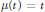
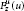
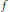

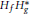
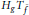
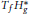
 , let
, let 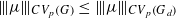 , for
, for 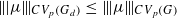 . These inequalities were already known for
. These inequalities were already known for 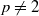 . Finally, for
. Finally, for 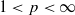 . We show here that this conjecture is false. Indeed for a large class of reflexive spaces, the above property characterizes Hilbert space.
. We show here that this conjecture is false. Indeed for a large class of reflexive spaces, the above property characterizes Hilbert space.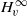 or
or 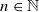 , bounded local
, bounded local 