Refine listing
Actions for selected content:
321 results in 47Bxx
Multidimensional Hausdorff operators on the real Hardy space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 79-86
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
A note on the boundedness of Bergman-type operators on mixed norm spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 395-402
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
On symmetric ideals of multilinear mappings between Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 141-148
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
On Generalized Schwarz-Pick Estimates
- Part of
-
- Journal:
- Mathematika / Volume 53 / Issue 1 / June 2006
- Published online by Cambridge University Press:
- 21 December 2009, pp. 161-168
- Print publication:
- June 2006
-
- Article
- Export citation
Some new Besov and Triebel-Lizorkin spaces associated with para-accretive functions on spaces of homogeneous type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-262
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
U-Operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 59-90
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
Composition operators in Orlicz spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-206
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Bilinear integration with positive vector measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 279-294
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
Solution of jump parameter systems of differential and difference equations with semi-Markov coefficients
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 442-454
- Print publication:
- June 2003
-
- Article
- Export citation
Biseparating linear maps between continuous vector-valued function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 101-110
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Moment sequences and backward extensions of subnormal weighted shifts
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 27-36
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
Strongly omnipresent operators: general conditions and applications to composition operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-348
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
On the Toeplitz algebras of right-angled and finite-type Artin groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-246
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Lacunarity on nonabelian groups and summing operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 71-79
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Diameter-preserving linear bijections of function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 323-336
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
Essentially commutative C*-algebras with essential spectrum homeomorphic to S2n−1
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-210
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
Composition operators on Qp spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 161-188
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
Integration maps and local equicontinuity of spectral measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 176-186
- Print publication:
- October 2000
-
- Article
-
- You have access
- Export citation
Weighted composition operators in weighted Banach spaces of analytic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 41-60
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
Generalized functions associated with self-adjoint operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-311
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
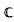 ” with an application to Gleason's problem.
” with an application to Gleason's problem.
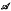
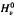 and
and 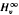 . we estimate the essential norm of a weighted composition operator and compute it for those Banach spaces
. we estimate the essential norm of a weighted composition operator and compute it for those Banach spaces 