Refine listing
Actions for selected content:
321 results in 47Bxx
Spectral and asymptotic properties of resolvent-dominated operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 181-201
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
The Möbius boundedness of the space Qp
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 373-378
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Boundedness of rough singular integral operators on homogeneous Herz spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 2 / April 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 201-223
- Print publication:
- April 1999
-
- Article
-
- You have access
- Export citation
The domain space of an analytic composition operator
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 56-65
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
Operators and the space of integrable scalar functions with respect to a Fréchet-valued measure
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 176-193
- Print publication:
- October 1998
-
- Article
-
- You have access
- Export citation
Composition operators between weighted Banach spaces of analytic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 101-118
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
Compact Toeplitz operators on weighted harmonic Bergman spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 136-148
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
Spectral and asymptotic properties of dominated operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 16-31
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
Algebraic characterizations of locally compact groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-420
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
Asymptotic behaviour of non-autonomous dissipative systems in Hilbert space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 1 / February 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 93-103
- Print publication:
- February 1997
-
- Article
-
- You have access
- Export citation
Measurable Hilbert sheaves
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-215
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
Some examples related to Kato's conjecture
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 274-286
- Print publication:
- April 1996
-
- Article
-
- You have access
- Export citation
Stationary distributions under mutation-selection balance: structure and properties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 227-251
- Print publication:
- March 1996
-
- Article
- Export citation
Toeplitz and Hankel type operators on an annulus
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 266-276
- Print publication:
- December 1994
-
- Article
- Export citation
Invariant subspaces in the bidisc and commutators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 232-242
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Toeplitz and Hankel type operators on Bergman space
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 345-356
- Print publication:
- December 1993
-
- Article
- Export citation
Generation of generators of holomorphic semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 246-269
- Print publication:
- October 1993
-
- Article
-
- You have access
- Export citation
The spectral theorem for well-bounded operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 3 / June 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 334-351
- Print publication:
- June 1993
-
- Article
-
- You have access
- Export citation
M-Cohyponormal powers of composition operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 9-16
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
Multiplication Operators and Dynamical Systems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 92-102
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
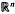 ) functions and Ricci-Stein oscillatory singular integral operators. Some new results are obtained.
) functions and Ricci-Stein oscillatory singular integral operators. Some new results are obtained.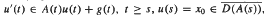 where {
where {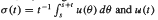 are weakly convergent.
are weakly convergent. *
*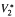 , For example, M is studied when the commutator is self-adjoint or of finite rank.
, For example, M is studied when the commutator is self-adjoint or of finite rank.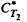 with respect to
with respect to 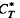 and
and 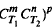 ]* is
]* is 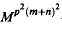 -hyponormal. As a consequence, we see that if
-hyponormal. As a consequence, we see that if 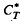 is an M-hyponormal composition operator, then
is an M-hyponormal composition operator, then 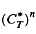 is
is 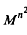 -hyponormal for all positive integers
-hyponormal for all positive integers 