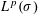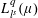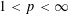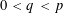Refine listing
Actions for selected content:
42 results in 47Gxx
Sharp Bounds for Oscillatory Integral Operators with Homogeneous Polynomial Phases
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 20 December 2019, pp. 771-786
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Maximal Operator for the Higher Order Calderón Commutator
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 03 September 2019, pp. 1386-1422
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Wave propagation for a class of non-local dispersal non-cooperative systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 14 March 2019, pp. 1965-1997
- Print publication:
- August 2020
-
- Article
- Export citation
Strong maximum principles for fractional elliptic and parabolic problems with mixed boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 475-495
- Print publication:
- February 2020
-
- Article
- Export citation
Pseudo-differential operators with nonlinear quantizing functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 103-130
- Print publication:
- February 2020
-
- Article
-
- You have access
- Open access
- Export citation
ON THE BILINEAR SQUARE FOURIER MULTIPLIER OPERATORS ASSOCIATED WITH
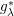 $g_{\unicode[STIX]{x1D706}}^{\ast }$ FUNCTION
$g_{\unicode[STIX]{x1D706}}^{\ast }$ FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 28 August 2018, pp. 123-152
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
FRACTIONAL INTEGRAL OPERATORS ON
 $\unicode[STIX]{x1D6FC}$ -MODULATION SPACES IN THE FULL RANGE
$\unicode[STIX]{x1D6FC}$ -MODULATION SPACES IN THE FULL RANGE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 499-512
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
GENERALIZED HARDY–CESÀRO OPERATORS BETWEEN WEIGHTED SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 28 January 2018, pp. 13-24
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
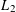 $L_{2}$ -SMALL DEVIATIONS FOR WEIGHTED STATIONARY PROCESSES
$L_{2}$ -SMALL DEVIATIONS FOR WEIGHTED STATIONARY PROCESSES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 387-405
- Print publication:
- 2018
-
- Article
- Export citation
A NOTE ON MARCINKIEWICZ INTEGRALS ASSOCIATED TO SURFACES OF REVOLUTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 380-402
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
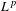 $L^{p}$-BOUNDS FOR PSEUDO-DIFFERENTIAL OPERATORS ON COMPACT LIE GROUPS
$L^{p}$-BOUNDS FOR PSEUDO-DIFFERENTIAL OPERATORS ON COMPACT LIE GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 03 April 2017, pp. 531-559
- Print publication:
- May 2019
-
- Article
-
- You have access
- Open access
- Export citation
Iterating Bilinear Hardy Inequalities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 955-971
-
- Article
- Export citation
Multiple solutions for a critical fractional elliptic system involving concave–convex nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 27 October 2016, pp. 1167-1193
- Print publication:
- December 2016
-
- Article
- Export citation
TWO-WEIGHT NORM INEQUALITIES FOR VECTOR-VALUED OPERATORS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 July 2016, pp. 72-91
- Print publication:
- 2017
-
- Article
- Export citation
Linear non-local diffusion problems in metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 833-863
- Print publication:
- August 2016
-
- Article
- Export citation
On Nonlinear Boundary Conditions Involving Decomposable Linear Functionals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 421-439
-
- Article
-
- You have access
- Export citation
MIXED NORM INEQUALITIES FOR SOME DIRECTIONAL MAXIMAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 448-455
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
UNIQUENESS OF TRACES ON LOG-POLYHOMOGENEOUS PSEUDODIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 31 May 2011, pp. 171-181
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
FRACTIONAL INTEGRAL OPERATORS IN NONHOMOGENEOUS SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 29 June 2009, pp. 324-334
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
U-Operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 59-90
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
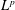
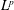
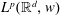
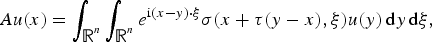
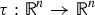
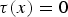
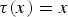
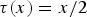
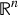
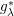

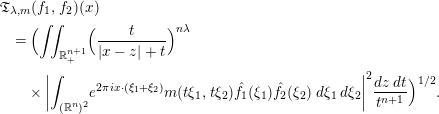
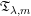
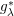
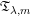
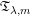


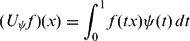
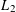
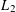
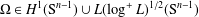
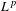
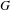
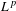
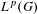
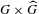
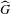
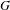
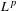
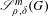
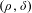
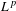
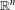
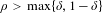
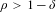
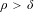
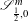
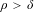
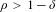
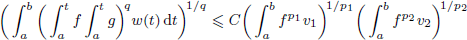
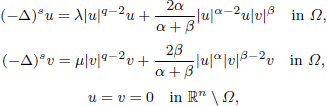
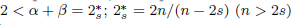 is the fractional critical Sobolev exponent.
is the fractional critical Sobolev exponent.