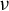Refine listing
Actions for selected content:
16 results in 34Fxx
Averaging principle for the fast–slow McKean–Vlasov stochastic differential equations driven by mixed fractional Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 05 June 2025, pp. 1-20
-
- Article
- Export citation
Pullback measure attractors for non-autonomous stochastic lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-20
-
- Article
- Export citation
Flocking dynamics of agents moving with a constant speed and a randomly switching topology
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 30 April 2024, pp. 419-447
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MODELLING WATER QUALITY WITH STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 09 January 2024, pp. 273-284
-
- Article
- Export citation
Statistical determinism in non-Lipschitz dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1856-1884
- Print publication:
- July 2024
-
- Article
- Export citation
Asymptotics of quasi-stationary distributions of small noise stochastic dynamical systems in unbounded domains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 64-110
- Print publication:
- March 2022
-
- Article
- Export citation
On the stochastic resonance phenomenon in parametrically excited systems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 26 September 2018, pp. 986-1003
-
- Article
- Export citation
EXACT ANALYTICAL EXPRESSIONS FOR THE FINAL EPIDEMIC SIZE OF AN SIR MODEL ON SMALL NETWORKS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 429-444
-
- Article
-
- You have access
- Export citation
Some Remarks on Davie’s Uniqueness Theorem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 1019-1035
-
- Article
- Export citation
Convergence of Achlioptas Processes via Differential Equations with Unique Solutions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 14 October 2015, pp. 154-171
-
- Article
- Export citation
Corrigendum: On the use of a discrete form of the Itô formula in the article ‘Almost sure asymptotic stability analysis of the
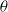 $\theta $ -Maruyama method applied to a test system with stabilising and destabilising stochastic perturbations’
$\theta $ -Maruyama method applied to a test system with stabilising and destabilising stochastic perturbations’
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 September 2013, pp. 366-372
-
- Article
-
- You have access
- Export citation
Almost sure asymptotic stability analysis of the θ-Maruyama method applied to a test system with stabilising and destabilising stochastic perturbations
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 April 2012, pp. 71-83
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC BEHAVIOUR OF RANDOM MARKOV CHAINS WITH TRIDIAGONAL GENERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 30 March 2012, pp. 27-36
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
Solution of jump parameter systems of differential and difference equations with semi-Markov coefficients
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 442-454
- Print publication:
- June 2003
-
- Article
- Export citation
Stochastic non-linear oscillators
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 649-666
- Print publication:
- September 1993
-
- Article
- Export citation
Uniqueness and non-uniqueness of solutions of Vlasov-McKean equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 246-256
- Print publication:
- October 1987
-
- Article
-
- You have access
- Export citation