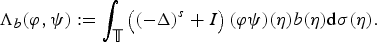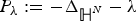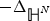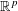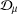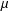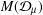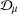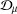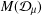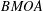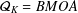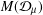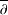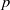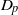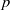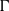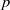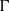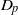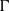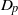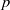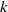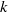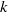Refine listing
Actions for selected content:
42 results in 31Cxx
New sharp Hardy and Rellich type inequalities on Cartan–Hadamard manifolds and their improvements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 2952-2981
- Print publication:
- December 2020
-
- Article
- Export citation
Bilinear forms on potential spaces in the unit circle
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 19 March 2019, pp. 2117-2154
- Print publication:
- August 2020
-
- Article
- Export citation
An optimal improvement for the Hardy inequality on the hyperbolic space and related manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1699-1736
- Print publication:
- August 2020
-
- Article
- Export citation
Monotonicity of non-Liouville property for positive solutions of skew product elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1429-1449
- Print publication:
- June 2020
-
- Article
- Export citation
Existence and non-existence of minimal graphic and p-harmonic functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 25 January 2019, pp. 341-366
- Print publication:
- February 2020
-
- Article
- Export citation
Geometry of Uniform Spanning Forest Components in High Dimensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1297-1321
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
ANALYSIS IN THE MULTI-DIMENSIONAL BALL
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 190-212
- Print publication:
- 2019
-
- Article
- Export citation
ASYMPTOTIC LINEAR PROGRAMMING LOWER BOUNDS FOR THE ENERGY OF MINIMIZING RIESZ AND GAUSS CONFIGURATIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 27 September 2018, pp. 157-180
- Print publication:
- 2019
-
- Article
- Export citation
MÖBIUS INVARIANT FUNCTION SPACES AND DIRICHLET SPACES WITH SUPERHARMONIC WEIGHTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 12 July 2018, pp. 1-18
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Evaluating the Origin Intensity Factor in the Singular Boundary Method for Three-Dimensional Dirichlet Problems
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1289-1311
- Print publication:
- December 2017
-
- Article
- Export citation
LANDAU’S THEOREM FOR SOLUTIONS OF THE
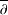 $\overline{\unicode[STIX]{x2202}}$ -EQUATION IN DIRICHLET-TYPE SPACES
$\overline{\unicode[STIX]{x2202}}$ -EQUATION IN DIRICHLET-TYPE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 28 September 2017, pp. 80-87
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
DASHMM: Dynamic Adaptive System for Hierarchical Multipole Methods
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 1106-1126
- Print publication:
- October 2016
-
- Article
- Export citation
RECFMM: Recursive Parallelization of the Adaptive Fast Multipole Method for Coulomb and Screened Coulomb Interactions
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 2 / August 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 534-550
- Print publication:
- August 2016
-
- Article
- Export citation
COEFFICIENT ESTIMATES, LANDAU’S THEOREM AND LIPSCHITZ-TYPE SPACES ON PLANAR HARMONIC MAPPINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 198-215
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
THE
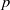 $p$-HARMONIC BOUNDARY AND
$p$-HARMONIC BOUNDARY AND 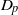 ${D}_{p} $-MASSIVE SUBSETS OF A GRAPH OF BOUNDED DEGREE
${D}_{p} $-MASSIVE SUBSETS OF A GRAPH OF BOUNDED DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 12 June 2013, pp. 149-158
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
WEAK CONTINUITY OF THE COMPLEX
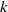 $k$-HESSIAN OPERATORS WITH RESPECT TO LOCAL UNIFORM CONVERGENCE
$k$-HESSIAN OPERATORS WITH RESPECT TO LOCAL UNIFORM CONVERGENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 11 June 2013, pp. 227-233
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
ASPECTS OF RECURRENCE AND TRANSIENCE FOR LÉVY PROCESSES IN TRANSFORMATION GROUPS AND NONCOMPACT RIEMANNIAN SYMMETRIC PAIRS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 31 May 2013, pp. 304-320
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Convergence of Brownian motion with a scaled Dirac delta potential
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 403-427
-
- Article
-
- You have access
- Export citation
TWO NONTRIVIAL WEAK SOLUTIONS FOR THE DIRICHLET PROBLEM ON THE SIERPIŃSKI GASKET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 12 December 2011, pp. 395-414
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
DISTANCE GEOMETRY IN QUASIHYPERMETRIC SPACES. I
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 19 June 2009, pp. 1-25
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation