Refine listing
Actions for selected content:
1821 results in 60Gxx
On an optimal extraction problem with regime switching
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 671-705
- Print publication:
- September 2018
-
- Article
- Export citation
Windings of planar processes, exponential functionals and Asian options
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 726-742
- Print publication:
- September 2018
-
- Article
- Export citation
Characterization and simplification of optimal strategies in positive stochastic games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 728-741
- Print publication:
- September 2018
-
- Article
- Export citation
MODELLING JOINT AUTOREGRESSIVE MOVING AVERAGE PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 345-347
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
ON THE WEAK-HASH METRIC FOR BOUNDEDLY FINITE INTEGER-VALUED MEASURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 265-276
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
On perpetuities with gamma-like tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 368-389
- Print publication:
- June 2018
-
- Article
- Export citation
Stochastic nonzero-sum games: a new connection between singular control and optimal stopping
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 347-372
- Print publication:
- June 2018
-
- Article
- Export citation
Uniqueness for measure-valued equations of nonlinear filtering for stochastic dynamical systems with Lévy noise
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 396-413
- Print publication:
- June 2018
-
- Article
- Export citation
Weighted least-squares estimation for the subcritical Heston process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 543-558
- Print publication:
- June 2018
-
- Article
- Export citation
General drawdown-based de Finetti optimization for spectrally negative Lévy risk processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 513-542
- Print publication:
- June 2018
-
- Article
- Export citation
Joint distribution of a Lévy process and its running supremum
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 488-512
- Print publication:
- June 2018
-
- Article
- Export citation
On the Mabinogion urn model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 327-346
- Print publication:
- June 2018
-
- Article
- Export citation
Exact moderate and large deviations for linear random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 431-449
- Print publication:
- June 2018
-
- Article
- Export citation
Local asymptotics for the area under the random walk excursion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 600-620
- Print publication:
- June 2018
-
- Article
- Export citation
First-passage time asymptotics over moving boundaries for random walk bridges
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 627-651
- Print publication:
- June 2018
-
- Article
- Export citation
A weighted weak-type bound for Haar multipliers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 643-658
- Print publication:
- June 2018
-
- Article
- Export citation
On a jump-telegraph process driven by an alternating fractional Poisson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 94-111
- Print publication:
- March 2018
-
- Article
- Export citation
A conjecture on the Feldman bandit problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 318-324
- Print publication:
- March 2018
-
- Article
- Export citation
A large sample test for the length of memory of stationary symmetric stable random fields via nonsingular ℤd-actions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 179-195
- Print publication:
- March 2018
-
- Article
- Export citation
Stein's method for negatively associated random variables with applications to second-order stationary random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 196-215
- Print publication:
- March 2018
-
- Article
- Export citation
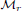 is the
is the