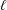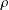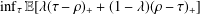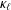Refine listing
Actions for selected content:
1827 results in 60Gxx
Potential kernel, hitting probabilities and distributional asymptotics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1894-1967
- Print publication:
- July 2020
-
- Article
- Export citation
On the modified Palm version
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 271-280
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Occupation times of alternating renewal processes with Lévy applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1287-1308
- Print publication:
- December 2018
-
- Article
- Export citation
Partisan gerrymandering with geographically compact districts
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1046-1059
- Print publication:
- December 2018
-
- Article
- Export citation
The sequential loss of allelic diversity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 13-29
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Preferential attachment graphs with co-existing types of different fitnesses
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1211-1227
- Print publication:
- December 2018
-
- Article
- Export citation
Weak convergence of the number of vertices at intermediate levels of random recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1131-1142
- Print publication:
- December 2018
-
- Article
- Export citation
An asymmetric St. Petersburg game with trimming
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 115-129
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Pathwise large deviations for the rough Bergomi model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1078-1092
- Print publication:
- December 2018
-
- Article
- Export citation
On optimal periodic dividend and capital injection strategies for spectrally negative Lévy models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1272-1286
- Print publication:
- December 2018
-
- Article
- Export citation
Exit times for ARMA processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 191-195
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Nearest-neighbour Markov point processes on graphs with Euclidean edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1275-1293
- Print publication:
- December 2018
-
- Article
- Export citation
Linear de-preferential urn models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1176-1192
- Print publication:
- December 2018
-
- Article
- Export citation
Branching-stable point measures and processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1294-1314
- Print publication:
- December 2018
-
- Article
- Export citation
Efficient simulation of Brown‒Resnick processes based on variance reduction of Gaussian processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1155-1175
- Print publication:
- December 2018
-
- Article
- Export citation
Assouad Dimension of Random Processes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 281-290
-
- Article
- Export citation
On the stochastic dynamics of a nonlinear vibration energy harvester driven by Lévy flight excitations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 08 October 2018, pp. 945-967
-
- Article
- Export citation
OPTIMAL STOPPING FOR THE LAST EXIT TIME
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 04 October 2018, pp. 148-160
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Equivariant thinning over a free group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 25 September 2018, pp. 1057-1067
- Print publication:
- April 2020
-
- Article
- Export citation
Furstenberg entropy of intersectional invariant random subgroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 17 September 2018, pp. 2239-2265
- Print publication:
- October 2018
-
- Article
- Export citation