Refine listing
Actions for selected content:
1827 results in 60Gxx
Nonstationarity in ℝn is second-order stationarity in ℝ2n
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 815-820
- Print publication:
- September 2003
-
- Article
- Export citation
From the central limit theorem to heavy-tailed distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 803-806
- Print publication:
- September 2003
-
- Article
- Export citation
A method for computing total downtime distributions in repairable systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 643-653
- Print publication:
- September 2003
-
- Article
- Export citation
A note on the full-information Poisson arrival selection problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1147-1154
- Print publication:
- September 2003
-
- Article
- Export citation
Random coefficient autoregression, regime switching and long memory
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 737-754
- Print publication:
- September 2003
-
- Article
- Export citation
Generalized Lorenz curves and convexifications of stochastic processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 906-925
- Print publication:
- September 2003
-
- Article
- Export citation
Optimal reward on a sparse tree with random edge weights
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 926-945
- Print publication:
- September 2003
-
- Article
- Export citation
Shot noise Cox processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 614-640
- Print publication:
- September 2003
-
- Article
- Export citation
Brownian excursions and Parisian barrier options: a note
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 855-864
- Print publication:
- September 2003
-
- Article
- Export citation
On moments and tail behaviors of storage processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1069-1086
- Print publication:
- September 2003
-
- Article
- Export citation
Almost sure relative stability of the maximum of a stationary sequence
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 721-736
- Print publication:
- September 2003
-
- Article
- Export citation
Exact overflow asymptotics for queues with many Gaussian inputs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 704-720
- Print publication:
- September 2003
-
- Article
- Export citation
Probabilité de ruine éventuelle dans un modèle de risque à temps discret
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 543-556
- Print publication:
- September 2003
-
- Article
- Export citation
Statistical properties of a system reliability estimator using the Littlewood software reliability model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 766-778
- Print publication:
- September 2003
-
- Article
- Export citation
Characterizations using record moments in a random record model and applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 826-833
- Print publication:
- September 2003
-
- Article
- Export citation
Local convergence of the Boolean shell model towards the thick Poisson hyperplane process in the Euclidean space
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 354-361
- Print publication:
- June 2003
-
- Article
- Export citation
Palm representation and approximation of the covariance of random closed sets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 295-302
- Print publication:
- June 2003
-
- Article
- Export citation
Stationary iterated tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 337-353
- Print publication:
- June 2003
-
- Article
- Export citation
Haplotypes: the joint distribution of alleles at linked loci
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 505-512
- Print publication:
- June 2003
-
- Article
- Export citation
An improved approximation for assessing the statistical significance of molecular sequence features
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 427-441
- Print publication:
- June 2003
-
- Article
- Export citation
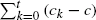 is bounded as the time
is bounded as the time 