Refine listing
Actions for selected content:
1827 results in 60Gxx
Overshoots over curved boundaries
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 417-448
- Print publication:
- June 2003
-
- Article
- Export citation
The nature of discrete second-order self-similarity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 395-416
- Print publication:
- June 2003
-
- Article
- Export citation
Precise large deviations for the prospective-loss process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 391-400
- Print publication:
- June 2003
-
- Article
- Export citation
Inhomogeneous spatial point processes by location-dependent scaling
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 319-336
- Print publication:
- June 2003
-
- Article
- Export citation
An exponential functional of random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 413-426
- Print publication:
- June 2003
-
- Article
- Export citation
Frailty models based on Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 532-550
- Print publication:
- June 2003
-
- Article
- Export citation
Fully coupled FBSDE with Brownian motion and Poisson process in stopping time duration
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-266
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Decomposition of gamma-distributed domains constructed from Poisson point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 56-69
- Print publication:
- March 2003
-
- Article
- Export citation
Bayesian analysis of deformed tessellation models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 4-26
- Print publication:
- March 2003
-
- Article
- Export citation
On the integral of the workload process of the single server queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 200-225
- Print publication:
- March 2003
-
- Article
- Export citation
A new graph related to the directions of nearest neighbours in a point process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 47-55
- Print publication:
- March 2003
-
- Article
- Export citation
Optimal stopping on patterns in strings generated by independent random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 49-72
- Print publication:
- March 2003
-
- Article
- Export citation
Distance measurements on processes of flats
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 70-95
- Print publication:
- March 2003
-
- Article
- Export citation
Thick and thin points for random recursive fractals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 251-277
- Print publication:
- March 2003
-
- Article
- Export citation
Recursive filters for a partially observable system subject to random failure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 207-227
- Print publication:
- March 2003
-
- Article
- Export citation
Limits of sequences of stationary planar tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 123-138
- Print publication:
- March 2003
-
- Article
- Export citation
On the geometry of Lp (μ) with applications to infinite variance processes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 35-42
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Random patterns of nonoverlapping convex grains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 718-738
- Print publication:
- December 2002
-
- Article
- Export citation
The distributions of the smallest disks containing the Poisson-Voronoi typical cell and the Crofton cell in the plane
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 702-717
- Print publication:
- December 2002
-
- Article
- Export citation
Periodic Ornstein-Uhlenbeck processes driven by Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 748-763
- Print publication:
- December 2002
-
- Article
- Export citation
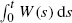 .
.