Refine listing
Actions for selected content:
1827 results in 60Gxx
A martingale approach to strong convergence of the number of records
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 864-873
- Print publication:
- December 2001
-
- Article
- Export citation
Testing for signals with unknown location and scale in a χ2 random field, with an application to fMRI
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 773-793
- Print publication:
- December 2001
-
- Article
- Export citation
On the asymptotic relationship between the overflow probability and the loss ratio
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 836-863
- Print publication:
- December 2001
-
- Article
- Export citation
On filtering in Markovian term structure models: an approximation approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 794-809
- Print publication:
- December 2001
-
- Article
- Export citation
A probabilistic method for Navier-Stokes vortices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1059-1066
- Print publication:
- December 2001
-
- Article
- Export citation
Availability analysis of periodically inspected systems with random walk model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 860-871
- Print publication:
- December 2001
-
- Article
- Export citation
Central limit theorem for germination-growth models in ℝd with non-Poisson locations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 751-755
- Print publication:
- December 2001
-
- Article
- Export citation
The number of two-dimensional maxima
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 727-750
- Print publication:
- December 2001
-
- Article
- Export citation
Exact asymptotics for a queue with fractional Brownian input and applications in ATM networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 932-945
- Print publication:
- December 2001
-
- Article
- Export citation
Optimal estimation of diffusion processes hidden by general obstacles
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1067-1073
- Print publication:
- December 2001
-
- Article
- Export citation
Lagrangian observations of homogeneous random environments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 810-835
- Print publication:
- December 2001
-
- Article
- Export citation
Generalized vector multiplicative cascades
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 874-895
- Print publication:
- December 2001
-
- Article
- Export citation
Optimal stopping on trajectories and the ballot problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 946-959
- Print publication:
- December 2001
-
- Article
- Export citation
Sequential games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1006-1017
- Print publication:
- December 2001
-
- Article
- Export citation
On some distributional properties of a first-order nonnegative bilinear time series model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 659-671
- Print publication:
- September 2001
-
- Article
- Export citation
On hitting times for compound Poisson dams with exponential jumps and linear release rate
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 781-786
- Print publication:
- September 2001
-
- Article
- Export citation
Calculation of noncrossing probabilities for Poisson processes and its corollaries
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 702-716
- Print publication:
- September 2001
-
- Article
- Export citation
On the total time spent in records by a discrete uniform sequence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 768-775
- Print publication:
- September 2001
-
- Article
- Export citation
Analogies and correspondences between variograms and covariance functions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 617-630
- Print publication:
- September 2001
-
- Article
- Export citation
On the rose of intersections of stationary flat processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 584-599
- Print publication:
- September 2001
-
- Article
- Export citation
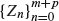 . This problem is closely related to the celebrated ballot problem, so that we obtain some identities concerning the ballot problem and then derive the optimal stopping rule explicitly. Some related modifications are also studied.
. This problem is closely related to the celebrated ballot problem, so that we obtain some identities concerning the ballot problem and then derive the optimal stopping rule explicitly. Some related modifications are also studied.