We investigate an optimal stopping time problem which arises from pricing Russian options (i.e. perpetual look-back options) on a stock whose price fluctuations are modelled by adjoining a hidden Markov process to the classical Black-Scholes geometric Brownian motion model. By extending the technique of smooth fit to allow jump discontinuities, we obtain an explicit closed-form solution. It gives a non-standard application of the well-known smooth fit principle where the optimal strategy involves jumping over the optimal boundary and by an arbitrary overshoot. Based on the optimal stopping analysis, an arbitrage-free price for Russian options under the hidden Markov model is derived.

A new computationally simple, speedy and accurate method is proposed to construct first-passage-time probability density functions for Gauss–Markov processes through time-dependent boundaries, both for fixed and for random initial states. Some applications to Brownian motion and to the Brownian bridge are then provided together with a comparison with some computational results by Durbin and by Daniels. Various closed-form results are also obtained for classes of boundaries that are intimately related to certain symmetries of the processes considered.

Intrinsic volumes are key functionals in convex geometry and have also appeared in several stochastic settings. Here we relate them to questions of regularity in Gaussian processes with regard to Itô–Nisio oscillation and metrization of GB/GC indexing sets. Various bounds and estimates are presented, and questions for further investigation are suggested. From alternate points of view, much of the discussion can be interpreted in terms of (i) random sets and (ii) properties of (deterministic) infinite-dimensional convex bodies.

This paper analyzes optimal single and multiple stopping rules for a class of correlated random walks that provides an elementary model for processes exhibiting momentum or directional reinforcement behavior. Explicit descriptions of optimal stopping rules are given in several interesting special cases with and without transaction costs. Numerical examples are presented comparing optimal strategies to simpler buy and hold strategies.

We define and analyse a random coverage process of the d-dimensional Euclidean space which allows us to describe a continuous spectrum that ranges from the Boolean model to the Poisson–Voronoi tessellation to the Johnson–Mehl model. As for the Boolean model, the minimal stochastic setting consists of a Poisson point process on this Euclidean space and a sequence of real valued random variables considered as marks of this point process. In this coverage process, the cell attached to a point is defined as the region of the space where the effect of the mark of this point exceeds an affine function of the cumulative effect of all marks. This cumulative effect is defined as the shot-noise process associated with the marked point process. In addition to analysing and visualizing this spectrum, we study various basic properties of the coverage process such as the probability that a point or a pair of points be covered by a typical cell. We also determine the distribution of the number of cells which cover a given point, and show how to provide deterministic bounds on this number. Finally, we also analyse convergence properties of the coverage process using the framework of closed sets, and its differentiability properties using perturbation analysis. Our results require a pathwise continuity property for the shot-noise process for which we provide sufficient conditions. The model in question stems from wireless communications where several antennas share the same (or different but interfering) channel(s). In this case, the area where the signal of a given antenna can be received is the area where the signal to interference ratio is large enough. We describe this class of problems in detail in the paper. The results obtained allow us to compute quantities of practical interest within this setting: for instance the outage probability is obtained as the complement of the volume fraction; the law of the number of cells covering a point allows us to characterize handover strategies, and so on.

Let X = (X(t):t ≥ 0) be a Lévy process and X ∊ the compensated sum of jumps not exceeding ∊ in absolute value, σ2(∊) = var(X ∊(1)). In simulation, X - X ∊ is easily generated as the sum of a Brownian term and a compound Poisson one, and we investigate here when X ∊/σ(∊) can be approximated by another Brownian term. A necessary and sufficient condition in terms of σ(∊) is given, and it is shown that when the condition fails, the behaviour of X ∊/σ(∊) can be quite intricate. This condition is also related to the decay of terms in series expansions. We further discuss error rates in terms of Berry-Esseen bounds and Edgeworth approximations.

We present a stochastic algorithm which generates optimal probabilities for the chaos game to decompress an image represented by the fixed point of an IFS operator. The algorithm can be seen as a sort of time-inhomogeneous regenerative process. We prove that optimal probabilities exist and, by martingale methods, that the algorithm converges almost surely. The method holds for IFS operators associated with any arbitrary number of possibly overlapping affine contraction maps on the pixels space.

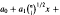
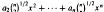An asymptotic estimate is derived for the expected number of extrema of a polynomial whose independent normal coefficients possess non-equal non-zero mean values. A result is presented that generalizes in terms of normal processes the analytical device used for construction of similar asymptotic estimates for random polynomials with normal coefficients.

In this paper, we consider the stochastic sequence {Y t }t∊ℕ defined recursively by the linear relation Y t+1 = A t Y t + B t in a random environment which is described by the non-stationary process {(A t , B t )}t∊ℕ. We formulate sufficient conditions on the environment which ensure that the finite-dimensional distributions of {Y t }t∊ℕ converge weakly to the finite-dimensional distributions of a unique stationary process. If the driving sequence {(A t , B t )}t∊ℕ becomes stationary in the long run, then we can establish a global convergence result. This extends results of Brandt (1986) and Borovkov (1998) from the stationary to the non-stationary case.

Let us consider n stocks with dependent price processes each following a geometric Brownian motion. We want to investigate the American perpetual put on an index of those stocks. We will provide inner and outer boundaries for its early exercise region by using a decomposition technique for optimal stopping.

Consider the Boolean model in ℝ2, where the germs form a homogeneous Poisson point process with intensity λ and the grains are convex compact random sets. It is known (see, e.g., Cressie (1993, Section 9.5.3)) that Laslett's rule transforms the exposed tangent points of the Boolean model into a homogeneous Poisson process with the same intensity. In the present paper, we give a simple proof of this result, which is based on a martingale argument. We also consider the cumulative process of uncovered area in a vertical strip and show that a (linear) Poisson process with intensity λ can be embedded in it.

We consider a system where units having magnitudes arrive according to a nonhomogeneous Poisson process, remain there for a random period and then depart. Eventually, at any point in time only a portion of those units which have entered the system remain. Of interest are the finite time properties and limiting behaviors of the distribution of magnitudes among the units present in the system and among those which have departed from the system. We will derive limiting results for the empirical distribution of magnitudes among the active (departed) units. These results are also shown to extend to systems having stages or steps through which units must proceed. Examples are given to illustrate these results.

Let X (t) be a continuous two-dimensional stationary Gaussian process with mean zero, having a marginal density function p[x ] and covariance matrix R (t). Let Δ = {∂L ; L > 0} be a family of piecewise smooth boundaries of similar two-dimensional star-shaped regions ΓL . We show that, under two conditions on R (t), the asymptotic distribution of the duration of an excursion of X (t) outside ΓL , for large L, depends on the position of the maximum of p[x ] on ∂L and on whether R ′(0) is zero or not, should the maximum occur at a vertex. We obtain the asymptotic distributions of the duration of an excursion for each of the three cases that arise. We also generalise some results of Breitung (1994) on the asymptotic crossing rates of vector Gaussian processes.

We consider a reflected superposition of a Brownian motion and a compound Poisson process as a model for the workload process of a queueing system with two types of customers under heavy traffic. The distributions of the duration of a busy cycle and the maximum workload during a cycle are determined in closed form.

In this article, we prove the existence of critical Hawkes point processes with a finite average intensity, under a heavy-tail condition for the fertility rate which is related to a long-range dependence property. Criticality means that the fertility rate integrates to 1, and corresponds to the usual critical branching process, and, in the context of Hawkes point processes with a finite average intensity, it is equivalent to the absence of ancestors. We also prove an ergodic decomposition result for stationary critical Hawkes point processes as a mixture of critical Hawkes point processes, and we give conditions for weak convergence to stationarity of critical Hawkes point processes.

Some consequences of restarting stochastic search algorithms are studied. It is shown under reasonable conditions that restarting when certain patterns occur yields probabilities that the goal state has not been found by the nth epoch which converge to zero at least geometrically fast in n. These conditions are shown to hold for restarted simulated annealing employing a local generation matrix, a cooling schedule T n ∼ c/n and restarting after a fixed number r + 1 of duplications of energy levels of states when r is sufficiently large. For simulated annealing with logarithmic cooling these probabilities cannot decrease to zero this fast. Numerical comparisons between restarted simulated annealing and several modern variations on simulated annealing are also presented and in all cases the former performs better.

A given number of bullets will be fired sequentially in an attempt to destroy as many targets as possible from a fixed number of targets. The probability of destroying a target at each shot is known. After each shot, there is a report on the state for the target; destroyed or intact. The reports are subject to the usual two types of errors and the probabilities of making these errors are also known. This paper shows that the myopic decision strategy that picks the next target to be the one with the highest intact posterior probability is the optimal strategy.

In generalization of the well-known formulae for quermass densities of stationary and isotropic Boolean models, we prove corresponding results for densities of mixed volumes in the stationary situation and show how they can be used to determine the intensity of non-isotropic Boolean models Z in d-dimensional space for d = 2, 3, 4. We then consider non-stationary Boolean models and extend results of Fallert on quermass densities to densities of mixed volumes. In particular, we present explicit formulae for a planar inhomogeneous Boolean model with circular grains.

The (unoriented or oriented) mean normal measure of a stationary process of convex particles carries information on the mean shape of the particles and may, in particular, be useful for describing and detecting anisotropy of the particle process. This paper investigates the mean normal measure under the aspect of its determination from intersections, especially with lines or hyperplanes.

Wang and Pötzelberger (1997) derived an explicit formula for the probability that a Brownian motion crosses a one-sided piecewise linear boundary and used this formula to approximate the boundary crossing probability for general nonlinear boundaries. The present paper gives a sharper asymptotic upper bound of the approximation error for the formula, and generalizes the results to two-sided boundaries. Numerical computations are easily carried out using the Monte Carlo simulation method. A rule is proposed for choosing optimal nodes for the approximating piecewise linear boundaries, so that the corresponding approximation errors of boundary crossing probabilities converge to zero at a rate of O(1/n 2).