Refine listing
Actions for selected content:
1827 results in 60Gxx
Restarting search algorithms with applications to simulated annealing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 242-259
- Print publication:
- March 2001
-
- Article
- Export citation
Optimal sequential allocation with imperfect feedback information
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 248-254
- Print publication:
- March 2001
-
- Article
- Export citation
Densities of mixed volumes for Boolean models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 39-60
- Print publication:
- March 2001
-
- Article
- Export citation
On the mean normal measures of a particle process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 25-38
- Print publication:
- March 2001
-
- Article
- Export citation
Boundary crossing probability for Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 152-164
- Print publication:
- March 2001
-
- Article
- Export citation
Some asymptotic results for transient random walks with applications to insurance risk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 108-121
- Print publication:
- March 2001
-
- Article
- Export citation
An asymptotic expansion for the optimal stopping boundary in problems with non-linear costs of observation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 67-79
- Print publication:
- March 2001
-
- Article
- Export citation
Multivariate subordination, self-decomposability and stability
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 160-187
- Print publication:
- March 2001
-
- Article
- Export citation
Optimal repair/replacement policy for a general repair model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 206-222
- Print publication:
- March 2001
-
- Article
- Export citation
Path properties of the primitives of a Brownian motion
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 119-133
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
Exploratory analysis of earthquake clusters by likelihood-based trigger models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue A / 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 202-212
- Print publication:
- 2001
-
- Article
- Export citation
Relative quiescence within the Jiashi swarm in Xinjiang, China: an application of the ETAS point process model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue A / 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 213-221
- Print publication:
- 2001
-
- Article
- Export citation
An innovation approach to non-Gaussian time series analysis
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue A / 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 78-92
- Print publication:
- 2001
-
- Article
- Export citation
Point process modelling of reservoir-induced seismicity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue A / 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 232-242
- Print publication:
- 2001
-
- Article
- Export citation
Point process convergence of stochastic volatility processes with application to sample autocorrelation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue A / 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 93-104
- Print publication:
- 2001
-
- Article
- Export citation
On the statistics of the linked stress release model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue A / 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 176-187
- Print publication:
- 2001
-
- Article
- Export citation
Misspecified change-point estimation problem for a Poisson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue A / 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 122-130
- Print publication:
- 2001
-
- Article
- Export citation
Random fractals and probability metrics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 925-947
- Print publication:
- December 2000
-
- Article
- Export citation
The number and sum of near-maxima for thin-tailed populations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1100-1116
- Print publication:
- December 2000
-
- Article
- Export citation
Optimal strategy in a dice game
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1110-1116
- Print publication:
- December 2000
-
- Article
- Export citation
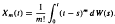 Watanabe and Lachal gave some asymptotic properties of the process
Watanabe and Lachal gave some asymptotic properties of the process 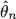 of
of 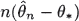 converges in law and in
converges in law and in 