Refine listing
Actions for selected content:
1705 results in 60Jxx
Distinguished exchangeable coalescents and generalized Fleming-Viot processes with immigration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 348-374
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Double-Barrier Parisian Options
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-20
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Irreducibility and continuity assumptions for positive operators with application to threshold GARCH time series models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 49-76
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Partial match queries in two-dimensional quadtrees: a probabilistic approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 178-194
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Limit theorems for supercritical age-dependent branching processes with neutral immigration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 276-300
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
An approximation for the inverse first passage time problem
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 264-275
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
The Probability of Containment for Multitype Branching Process Models for Emerging Epidemics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 173-188
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Multifractal spectra for random self-similar measures via branching processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-39
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
A General ‘Bang-Bang’ Principle for Predicting the Maximum of a Random Walk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1072-1083
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Approximations to quasi-birth-and-death processes with infinite blocks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1102-1125
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Limits of large metapopulations with patch-dependent extinction probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1172-1186
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Second-order properties and central limit theory for the vertex process of iteration infinitely divisible and iteration stable random tessellations in the plane
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 913-935
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
A Simple Model for Random Oscillations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1164-1173
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Information ranking and power laws on trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1057-1093
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
A Markov Model for the Spread of Viruses in an Open Population
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 976-996
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
On the First k Moments of the Random Count of a Pattern in a Multistate Sequence Generated by a Markov Source
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1105-1123
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Multiobjective Stopping Problem for Discrete-Time Markov Processes: Convex Analytic Approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 947-966
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Time reversal of some stationary jump diffusion processes from population genetics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1147-1171
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
New discount and average optimality conditions for continuous-time Markov decision processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 953-985
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Linear and Nonlinear Boundary Crossing Probabilities for Brownian Motion and Related Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1058-1071
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
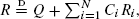 where
where 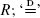 stands for equality in distribution. We study the asymptotic properties of the distribution of
stands for equality in distribution. We study the asymptotic properties of the distribution of 