Refine listing
Actions for selected content:
1705 results in 60Jxx
Markov Chains Conditioned Never to Wait Too Long at the Origin
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 812-826
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Fcfs infinite bipartite matching of servers and customers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 695-730
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Local Limit Approximations for Markov Population Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 690-708
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Limit Theorems for Random Triangular URN Schemes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 827-843
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Asymptotics of Iterated Branching Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 917-924
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
On the Transition Law of Tempered Stable Ornstein–Uhlenbeck Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 721-731
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Selective sweep and the size of the hitchhiking set
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 731-764
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Occupancy schemes associated to Yule processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 600-622
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
L Log L Criterion for a Class of Superdiffusions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 479-496
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Blackwell Optimality for Controlled Diffusion Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 372-391
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
A Two-Step Branching Splitting Model Under Cost Constraint for Rare Event Analysis
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 429-452
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
The Integral of the Supremum Process of Brownian Motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 593-600
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Similar States in Continuous-Time Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 497-506
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
A Weak Limit Theorem for Generalized Jiřina Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 453-462
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Fixed Precision MCMC Estimation by Median of Products of Averages
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 309-329
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Perturbed MAP Risk Models with Dividend Barrier Strategies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 521-541
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Quasi-Birth-and-Death Processes, Lattice Path Counting, and Hypergeometric Functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 507-520
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
The speed of extinction for some generalized jiřina processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 576-599
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Multitype Bienaymé–Galton–Watson processes escaping extinction
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 225-246
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Evolutionary prisoner's dilemma games with one-dimensional local interaction and imitation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 154-176
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
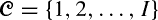 and an infinite sequence of servers of types
and an infinite sequence of servers of types 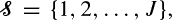 where a server of type
where a server of type 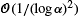 in total variation. Then, we use this framework to obtain an approximate distribution for the size of the hitchhiking set at the end of the selective sweep, with the same accuracy.
in total variation. Then, we use this framework to obtain an approximate distribution for the size of the hitchhiking set at the end of the selective sweep, with the same accuracy.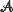 (
(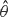 , i.e. an estimator which is a ‘median of products of averages’ (MPA). Sufficient conditions are given for
, i.e. an estimator which is a ‘median of products of averages’ (MPA). Sufficient conditions are given for 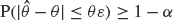 . Our main tool is a new bound on the mean-square error, valid also for nonreversible Markov chains on a finite state space.
. Our main tool is a new bound on the mean-square error, valid also for nonreversible Markov chains on a finite state space.