Refine listing
Actions for selected content:
1705 results in 60Jxx
COMPUTABLE STRONGLY ERGODIC RATES OF CONVERGENCE FOR CONTINUOUS-TIME MARKOV CHAINS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 463-478
-
- Article
-
- You have access
- Export citation
Transient Moments of the TCP Window Size Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 163-175
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Wiener-Hopf Factorization for Lévy Processes Having Positive Jumps with Rational Transforms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 118-134
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Weak Local Linear Discretizations for Stochastic Differential Equations with Jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 201-210
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
On a Comparison Result for Markov Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 279-286
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Law of Large Numbers for Dynamic Bargaining Markets
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 45-54
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Reduced Branching Processes with Very Heavy Tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 190-200
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
The Limit Behavior of Dual Markov Branching Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 176-189
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Identifiability of a Markovian model of molecular evolution with gamma-distributed rates
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 229-249
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Decay property of stopped Markovian bulk-arriving queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 95-121
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Nonexplosion of a class of semilinear equations via branching particle representations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 250-272
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Distributions of the Longest Excursions in a Tied Down Simple Random Walk and in a Brownian Bridge
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1056-1067
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Functional limit theorems for critical processes with immigration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1054-1069
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Long-Range Dependence of Markov Chains in Discrete Time on Countable State Space
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1047-1055
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Asymptotic Blocking Probabilities in Loss Networks with Subexponential Demands
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1088-1102
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Transformations of Galton-Watson processes and linear fractional reproduction
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1036-1053
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
On a Model for the Storage of Files on a Hardware. II. Evolution of a Typical Data Block
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 901-927
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Fixation in Conditional Branching Process Models in Population Genetics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1103-1110
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Numerically Optimized Markovian Coupling and Mixing in One-Dimensional Maps
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 161-181
- Print publication:
- December 2007
-
- Article
- Export citation
Asymptotic Behavior of a Generalized TCP Congestion Avoidance Algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 618-635
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
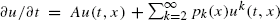 for
for 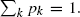 We obtain sufficient conditions for the existence of global positive solutions to semilinear equations of this form. Our results extend previous work by Nagasawa and Sirao (1969) and others.
We obtain sufficient conditions for the existence of global positive solutions to semilinear equations of this form. Our results extend previous work by Nagasawa and Sirao (1969) and others.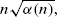 where α(
where α(