Refine listing
Actions for selected content:
1705 results in 60Jxx
Extinction Times in Multitype Markov Branching Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 296-307
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Bounds for the Ruin Probability of a Discrete-Time Risk Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 99-112
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Approximate probabilities for runs and patterns in i.i.d. and Markov-dependent multistate trials
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 292-308
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
An Optimal Dividends Problem with a Terminal Value for Spectrally Negative Lévy Processes with a Completely Monotone Jump Density
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 85-98
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Asymptotic Properties of a Mean-Field Model with a Continuous-State-Dependent Switching Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 221-243
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
On the First Passage time for Brownian Motion Subordinated by a Lévy Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 181-198
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Composition Markov chains of multinomial type
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 270-291
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Dependent Risk Models with Bivariate Phase-Type Distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 113-131
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
An Integral-Equation Approach for Defaultable Bond Prices with Application to Credit Spreads
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 71-84
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Expected coalescence time for a nonuniform allocation process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1002-1032
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
State-dependent importance sampling for regularly varying random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1104-1128
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Multiple-trial conflicts and stochastic evolutionary game dynamics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1174-1197
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Tails of Stopped Random Products: The Factoid and Some Relatives
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1161-1180
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
A Fourth Moment Inequality for Functionals of Stationary Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1086-1096
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Stochastic and substochastic solutions for infinite-state Markov chains with applications to matrix-analytic methods
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1157-1173
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
A Stochastic Volatility Alternative to SABR
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1071-1085
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Decentralized search on spheres using small-world Markov chains: expected hitting times and structural properties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 966-978
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Entry and Exit Decision Problem with Implementation Delay
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1039-1059
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
On level crossings for a general class of piecewise-deterministic Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 815-834
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Impact of Routeing on Correlation Strength in Stationary Queueing Network Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 846-878
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
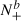 of upcrossings of some level
of upcrossings of some level 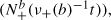 where ν
where ν