Refine listing
Actions for selected content:
1705 results in 60Jxx
Ergodic properties and ergodic decompositions of continuous-time Markov processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 767-781
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
The correlation of the maxima of correlated Brownian motions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 880-883
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
A matrix-analytic approach to the N-player ruin problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 755-766
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
On the exact asymptotics of the busy period in GI/G/1 queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 792-803
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
On the number of segregating sites for populations with large family sizes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 750-767
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Maximal avalanches in the Bak-Sneppen model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 840-851
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Searching for searchers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 899-904
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
A monotonicity in reversible Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 486-499
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
A central limit property under a modified Ehrenfest urn design
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 409-420
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Harmonic moments of inhomogeneous branching processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 465-486
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Moments of a Markov-modulated, irreducible network of fluid queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 510-522
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
On extreme ruinous behaviour of Lévy insurance risk processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 594-598
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Structured coalescent with nonconservative migration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 351-362
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Gambling Teams and Waiting Times for Patterns in Two-State Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 127-140
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
On the Waiting Time to Escape
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 296-302
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Local Linear Approximations of Jump Diffusion Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 185-194
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A Diffusion Limit for Generalized Correlated Random Walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 60-73
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Exact distribution of word counts in shuffled sequences
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 116-133
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A Limit Theorem for Discrete Galton-Watson Branching Processes with Immigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 289-295
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
An inhomogeneous semi-Markov model for the term structure of credit risk spreads
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 171-198
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
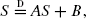 with specific independent random coefficients
with specific independent random coefficients 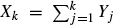 such that (
such that (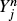 takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the
takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the 