We consider the M/M/∞ queue with m primary servers and infinitely many secondary servers. All the servers are numbered and ordered. An arriving customer takes the lowest available server. We define the wasted spaces as the difference between the highest numbered occupied server and the total number of occupied servers. Letting ρ = λ0/μ be the ratio of arrival to service rates, we study the probability distribution of the wasted spaces asymptotically for ρ → ∞. We also give some numerical results and the tail behavior for ρ = O(1).

We give a functional central limit theorem for spatial birth and death processes based on the representation of such processes as solutions of stochastic equations. For any bounded and integrable function in Euclidean space, we define a family of processes which is obtained by integrals of this function with respect to the centered and scaled spatial birth and death process with constant death rate. We prove that this family converges weakly to a Gaussian process as the scale parameter goes to infinity. We do not need the birth rates to have a finite range of interaction. Instead, we require that the birth rates have a range of interaction that decays polynomially. In order to show the convergence of the finite-dimensional distributions of the above processes, we extend Penrose's multivariate spatial central limit theorem. An example of the asymptotic normalities of the time-invariance estimators for the birth rates of spatial point processes is given.

In this paper we consider a compound Poisson risk model where the insurer earns credit interest at a constant rate if the surplus is positive and pays out debit interest at another constant rate if the surplus is negative. Absolute ruin occurs at the moment when the surplus first drops below a critical value (a negative constant). We study the asymptotic properties of the absolute ruin probability of this model. First we investigate the asymptotic behavior of the absolute ruin probability when the claim size distribution is light tailed. Then we study the case where the common distribution of claim sizes are heavy tailed.

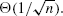We consider a multiserver queue in the Halfin-Whitt regime: as the number of servers n grows without a bound, the utilization approaches 1 from below at the rate Assuming that the service time distribution is lattice valued with a finite support, we characterize the limiting scaled stationary queue length distribution in terms of the stationary distribution of an explicitly constructed Markov chain. Furthermore, we obtain an explicit expression for the critical exponent for the moment generating function of a limiting stationary queue length. This exponent has a compact representation in terms of three parameters: the amount of spare capacity and the coefficients of variation of interarrival and service times. Interestingly, it matches an analogous exponent corresponding to a single-server queue in the conventional heavy-traffic regime.

The classical models in risk theory consider a single type of claim. In the insurance business, however, several business lines with separate claim arrival processes appear naturally, and the individual claim processes may not be independent. We introduce a new class of models for such situations, where the underlying counting process is a multivariate continuous-time Markov chain of pure-birth type and the dependency of the components arises from the fact that the birth rate for a specific claim type may depend on the number of claims in the other component processes. Under certain conditions, we obtain a fluid limit, i.e. a functional law of large numbers for these processes. We also investigate the consequences of such results for questions of interest in insurance applications. Several specific subclasses of the general model are discussed in detail and the Cramér asymptotics of the ruin probabilities are derived in particular cases.

We consider a model of random access (slotted-aloha-type) communication networks of general topology. Assuming that network links receive exogenous arrivals of packets for transmission, we seek dynamic distributed random access strategies whose goal is to keep all network queues stable. We prove that two dynamic strategies, which we collectively call queue length based random access (QRA), ensure stability as long as the rates of exogenous arrival flows are within the network saturation rate region. The first strategy, QRA-I, can be viewed as a random-access-model counterpart of the max-weight scheduling rule, while the second strategy, QRA-II, is a counterpart of the exponential (EXP) rule. The two strategies induce different dynamics of the queues in the fluid scaling limit, which can be exploited for the quality-of-service control in applications.

We consider an infectious disease spreading along the edges of a network which may have significant clustering. The individuals in the population have heterogeneous infectiousness and/or susceptibility. We define the out-transmissibility of a node to be the marginal probability that it would infect a randomly chosen neighbor given its infectiousness and the distribution of susceptibility. For a given distribution of out-transmissibility, we find the conditions which give the upper (or lower) bounds on the size and probability of an epidemic, under weak assumptions on the transmission properties, but very general assumptions on the network. We find similar bounds for a given distribution of in-transmissibility (the marginal probability of being infected by a neighbor). We also find conditions giving global upper bounds on the size and probability. The distributions leading to these bounds are network independent. In the special case of networks with high girth (locally tree-like), we are able to prove stronger results. In general, the probability and size of epidemics are maximal when the population is homogeneous and minimal when the variance of in- or out-transmissibility is maximal.

This paper is concerned with the characterization of weak-sense limits of state-dependent G-networks under heavy traffic. It is shown that, for a certain class of networks (which includes a two-layer feedforward network and two queues in tandem), it is possible to approximate the number of customers in the queue by a reflected stochastic differential equation. The benefits of such an approach are that it describes the transient evolution of these queues and allows the introduction of controls, inter alia. We illustrate the application of the results with numerical experiments.

We consider weak and strong survival for branching random walks on multigraphs with bounded degree. We prove that, at the strong critical value, the process dies out locally almost surely. We relate the weak critical value to a geometric parameter of the multigraph. For a large class of multigraphs (which enlarges the class of quasi-transitive or regular graphs), we prove that, at the weak critical value, the process dies out globally almost surely. Moreover, for the same class, we prove that the existence of a pure weak phase is equivalent to nonamenability. The results are extended to branching random walks on weighted graphs.

We consider a reflected Lévy process without negative jumps, starting at the origin. When the reflected process first upcrosses level K, a timer is activated. After D time units, the timer expires and the Lévy exponent of the Lévy process is changed. As soon as the process hits zero again, the Lévy exponent reverses to the original function. If the process has reached the origin before the timer expires then the Lévy exponent does not change. Using martingale techniques, we analyze the steady-state distribution of the resulting process, reflected at the origin. We pay special attention to the cases of deterministic and exponential timers, and to the following three special Lévy processes: (i) a compound Poisson process plus negative drift (corresponding to an M/G/1 queue), (ii) Brownian motion, and (iii) a Lévy process that is a subordinator until the timer expires.

We consider sequences of closed cycles of exponential single-server nodes with a single bottleneck. We study the cycle time and the successive sojourn times of a customer when the population sizes go to infinity. Starting from old results on the mean cycle times under heavy traffic conditions, we prove a central limit theorem for the cycle time distribution. This result is then utilised to prove a weak convergence characteristic of the vector of a customer's successive sojourn times during a cycle for a sequence of networks with population sizes going to infinity. The limiting picture is a composition of a central limit theorem for the bottleneck node and an exponential limit for the unscaled sequences of sojourn times for the nonbottleneck nodes.

In this paper we consider reflected diffusions with positive and negative jumps, constrained to lie in the nonnegative orthant of ℝn . We allow for the drift and diffusion coefficients, as well as for the directions of reflection, to be random fields over time and space. We provide a boundary behavior characterization, generalizing known results in the nonrandom coefficients and constant directions of the reflection case. In particular, the regulator processes are related to semimartingale local times at the boundaries, and they are shown not to charge the times the process expends at the intersection of boundary faces. Using the boundary results, we extend the conditions for product-form distributions in the stationary regime to the case when the drift and diffusion coefficients, as well as the directions of reflection, are random fields over space.

We study a flexible class of finite-disc process models with interaction between the discs. We let 𝒰 denote the random set given by the union of discs, and use for the disc process an exponential family density with the canonical sufficient statistic depending only on geometric properties of 𝒰 such as the area, perimeter, Euler-Poincaré characteristic, and the number of holes. This includes the quermass-interaction process and the continuum random-cluster model as special cases. Viewing our model as a connected component Markov point process, and thereby establishing local and spatial Markov properties, becomes useful for handling the problem of edge effects when only 𝒰 is observed within a bounded observation window. The power tessellation and its dual graph become major tools when establishing inclusion-exclusion formulae, formulae for computing geometric characteristics of 𝒰, and stability properties of the underlying disc process density. Algorithms for constructing the power tessellation of 𝒰 and for simulating the disc process are discussed, and the software is made public available.

The problem of finding the probability distribution of the first hitting time of a double integral process (DIP) such as the integrated Wiener process (IWP) has been an important and difficult endeavor in stochastic calculus. It has applications in many fields of physics (first exit time of a particle in a noisy force field) or in biology and neuroscience (spike time distribution of an integrate-and-fire neuron with exponentially decaying synaptic current). The only results available are an approximation of the stationary mean crossing time and the distribution of the first hitting time of the IWP to a constant boundary. We generalize these results and find an analytical formula for the first hitting time of the IWP to a continuous piecewise-cubic boundary. We use this formula to approximate the law of the first hitting time of a general DIP to a smooth curved boundary, and we provide an estimation of the convergence of this method. The accuracy of the approximation is computed in the general case for the IWP and the effective calculation of the crossing probability can be carried out through a Monte Carlo method.

We give a new method for simulating the time average steady-state distribution of a continuous-time queueing system, by extending a ‘read-once’ or ‘forward’ version of the coupling from the past (CFTP) algorithm developed for discrete-time Markov chains. We then use this to give a new proof of the ‘Poisson arrivals see time averages’ (PASTA) property, and a new proof for why renewal arrivals see either stochastically smaller or larger congestion than the time average if interarrival times are respectively new better than used in expectation (NBUE) or new worse than used in expectation (NWUE).

The TCP window size process can be modeled as a piecewise-deterministic Markov process that increases linearly and experiences downward jumps at Poisson times. We present a transient analysis of this window size process. Our main result is the Laplace transform of the transient moments. Formulae for the integer and fractional moments are derived, as well as an explicit characterization of the speed of convergence to steady state. Central to our approach are the infinitesimal generator and Dynkin's martingale.

In this paper we consider discrete-time multidimensional Markov chains having a block transition probability matrix which is the sum of a matrix with repeating block rows and a matrix of upper-Hessenberg, quasi-Toeplitz structure. We derive sufficient conditions for the existence of the stationary distribution, and outline two algorithms for calculating the stationary distribution.

We consider an independent long-range bond percolation on Z 2. Horizontal and vertical bonds of length n are independently open with probability p_n ∈ [0, 1]. Given ∑n=1 ∞∏i=1 n (1 − p i ) < ∞, we prove that there exists an infinite cluster of open bonds of length less than or equal to N for some large but finite N. The result gives a partial answer to the truncation problem.

We describe the random meeting motion of a finite number of investors in markets with friction as a Markov pure-jump process with interactions. Using a sequence of these, we prove a functional law of large numbers relating the large motions with the finite market of the so-called continuum of agents.

This paper presents new Gaussian approximations for the cumulative distribution function P(A λ ≤ s) of a Poisson random variable A λ with mean λ. Using an integral transformation, we first bring the Poisson distribution into quasi-Gaussian form, which permits evaluation in terms of the normal distribution function Φ. The quasi-Gaussian form contains an implicitly defined function y, which is closely related to the Lambert W-function. A detailed analysis of y leads to a powerful asymptotic expansion and sharp bounds on P(A λ ≤ s). 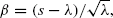The results for P(A λ ≤ s) differ from most classical results related to the central limit theorem in that the leading term Φ(β), with is replaced by Φ(α), where α is a simple function of s that converges to β as s tends to ∞. Changing β into α turns out to increase precision for small and moderately large values of s. The results for P(A λ ≤ s) lead to similar results related to the Erlang B formula. The asymptotic expansion for Erlang's B is shown to give rise to accurate approximations; the obtained bounds seem to be the sharpest in the literature thus far.