Refine listing
Actions for selected content:
1446 results in 60Kxx
Duality and Asymptotics for a Class of Nonneutral Discrete Moran Models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 866-893
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Threshold behaviour and final outcome of an epidemic on a random network with household structure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 765-796
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Limit Theorems for Random Triangular URN Schemes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 827-843
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Selective sweep and the size of the hitchhiking set
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 731-764
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
A Random Multiple-Access Protocol with Spatial Interactions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 844-865
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Optimal test Interval for a Monotone Safety System
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 330-341
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Occupancy schemes associated to Yule processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 600-622
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Double Optimal Stopping in the Fishing Problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 415-428
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Random transceiver networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 323-343
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Asymptotics for the moments of the overshoot and undershoot of a random walk
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 469-494
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Approximating Critical Parameters of Branching Random Walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 463-478
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
On Growth-Collapse Processes with Stationary Structure and Their Shot-Noise Counterparts
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 363-371
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Quasi-Birth-and-Death Processes, Lattice Path Counting, and Hypergeometric Functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 507-520
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
A Stochastic Model for Phylogenetic Trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 601-607
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
On a Terminating Shock Process with Independent Wear Increments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 353-362
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Bounds for the Ruin Probability of a Discrete-Time Risk Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 99-112
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Exponential Random Graphs as Models of Overlay Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 199-220
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Bounds for the Distance Between the Distributions of Sums of Absolutely Continuous i.i.d. Convex-Ordered Random Variables with Applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 255-271
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Lévy processes with adaptable exponent
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 177-205
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Optimal Allocation of Active Spares in Series Systems and Comparison of Component and System Redundancies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 19-34
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
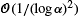 in total variation. Then, we use this framework to obtain an approximate distribution for the size of the hitchhiking set at the end of the selective sweep, with the same accuracy.
in total variation. Then, we use this framework to obtain an approximate distribution for the size of the hitchhiking set at the end of the selective sweep, with the same accuracy.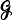 be the random directed graph with vertex set
be the random directed graph with vertex set 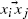 whenever
whenever 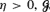 will almost surely have an infinite directed path, provided the expected number of transceivers that can receive a signal directly from
will almost surely have an infinite directed path, provided the expected number of transceivers that can receive a signal directly from 