Refine listing
Actions for selected content:
1446 results in 60Kxx
How fast can the chord length distribution decay?
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 504-523
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Contact Process with Destruction of Cubes and Hyperplanes: Forest Fires Versus Tornadoes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 352-365
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Exact Monte Carlo simulation for fork-join networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 484-503
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Phenotypic diversity and population growth in a fluctuating environment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 375-398
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Bounding basic characteristics of spatial epidemics with a new percolation model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 335-347
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Managing Queues with Heterogeneous Servers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 435-452
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Quasistationary Distributions and Fleming-Viot Processes in Finite Spaces
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 322-332
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Hitting Times and the Running Maximum of Markovian Growth-Collapse Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 295-312
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Concave Renewal Functions do not Imply DFR Interrenewal Times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 583-588
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
On the Markov Transition Kernels for First Passage Percolation on the Ladder
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 366-388
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
A Stochastic Breakdown Model for an Unreliable Web Server System and an Optimal Admission Control Policy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 453-466
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Simulation-Based Computation of the Workload Correlation Function in a Lévy-Driven Queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 114-130
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
On New Classes of Extreme Shock Models and Some Generalizations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 258-270
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Asymptotic Fluid Optimality and Efficiency of the Tracking Policy for Bandwidth-Sharing Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 90-113
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Large Deviations for the Graph Distance in Supercritical Continuum Percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 154-172
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Utility Optimization in Congested Queueing Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 68-89
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Matchmaking and Testing for Exponentiality in the M/G/∞ Queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 131-144
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
A Simple Model for Random Oscillations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1164-1173
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Information ranking and power laws on trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1057-1093
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
First Passage of a Markov Additive Process and Generalized Jordan Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1048-1057
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
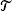 in environment
in environment 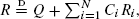 where
where 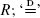 stands for equality in distribution. We study the asymptotic properties of the distribution of
stands for equality in distribution. We study the asymptotic properties of the distribution of 