Refine listing
Actions for selected content:
1446 results in 60Kxx
Implicit Renewal Theory and Power Tails on Trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 528-561
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On the Residual and Inactivity Times of the Components of Used Coherent Systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 385-404
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On the Transient Behavior of Ehrenfest and Engset Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 562-582
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Numerical Methods for the Exit Time of a Piecewise-Deterministic Markov Process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 196-225
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
A Recurrent Solution of PH/M/c/N-Like and PH/M/c-Like Queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 84-99
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Moderate Deviations for Stable Random Walks in Random Scenery
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 280-294
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Juggler's Exclusion Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 266-279
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Weak Convergence Limits for Closed Cyclic Networks of Queues with Multiple Bottleneck Nodes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 60-83
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Multiple-server system with flexible arrivals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 985-1004
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
On Λ-Coalescents with Dust Component
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1133-1151
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Percolation of Words on Z d with Long-Range Connections
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1152-1162
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Signatures of Coherent Systems Built with Separate Modules
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 843-855
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Heavy-Traffic Limits for Nearly Deterministic Queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 657-678
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Some Results for Vacation Systems with Sojourn Time Limits
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 679-687
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Signature-Based Representations for the Reliability of Systems with Heterogeneous Components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 856-867
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Asymptotic normality of the maximum likelihood estimator for cooperative sequential adsorption
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 636-648
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Geometry of the Poisson Boolean model on a region of logarithmic width in the plane
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 616-635
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Russo's Formula, Uniqueness of the Infinite Cluster, and Continuous Differentiability of Free Energy for Continuum Percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 597-610
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Stability of the exit time for Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 712-734
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Optimal Control of Capital Injections by Reinsurance with a Constant Rate of Interest
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 733-748
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
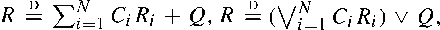 and similar recursions, where (
and similar recursions, where (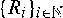 are independent and identically distributed copies of
are independent and identically distributed copies of 