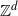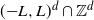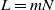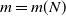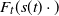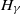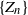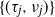Refine search
Actions for selected content:
52379 results in Statistics and Probability
Adaptation of a population to a changing environment in the light of quasi-stationarity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 235-286
- Print publication:
- March 2024
-
- Article
- Export citation
Multi-population mortality modelling: a Bayesian hierarchical approach
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 54 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 25 August 2023, pp. 46-74
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Understanding the impact of the COVID-19 pandemic response on GI infection surveillance trends in England, January 2020–April 2022
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 25 August 2023, e147
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fluconazole and echinocandin resistance of Candida species in invasive candidiasis at a university hospital during pre-COVID-19 and the COVID-19 outbreak
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 25 August 2023, e146
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Understanding the disease and economic impact of avirulent avian paramyxovirus type 1 (APMV-1) infection in Great Britain
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 25 August 2023, e163
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Typologies of duocentric networks among low-income newlywed couples
-
- Journal:
- Network Science / Volume 11 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 25 August 2023, pp. 632-656
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mortality associated with Omicron and influenza infections in France before and during the COVID-19 pandemic
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 25 August 2023, e148
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Algorithmic High-Dimensional Robust Statistics
-
- Published online:
- 24 August 2023
- Print publication:
- 07 September 2023
Detection and treatment of outliers for multivariate robust loss reserving
- Part of
-
- Journal:
- Annals of Actuarial Science / Volume 18 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 102-125
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interlacement limit of a stopped random walk trace on a torus
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 354-388
- Print publication:
- March 2024
-
- Article
- Export citation
Exchangeable FGM copulas
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 205-234
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Freedom and choice: public attitudes seven years on
-
- Journal:
- British Actuarial Journal / Volume 28 / 2023
- Published online by Cambridge University Press:
- 23 August 2023, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strong convergence of peaks over a threshold
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 August 2023, pp. 529-539
- Print publication:
- June 2024
-
- Article
- Export citation
Determinants of measles persistence in Beijing, China: A modelling study
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 22 August 2023, e144
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Branching processes in random environments with thresholds
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 495-544
- Print publication:
- June 2024
-
- Article
- Export citation
THE ESTIMATION RISK IN EXTREME SYSTEMIC RISK FORECASTS
-
- Journal:
- Econometric Theory / Volume 41 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 22 August 2023, pp. 341-390
-
- Article
-
- You have access
- Open access
- Export citation
Optimising rabies vaccination of dogs in India
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 22 August 2023, e164
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable systems with power law conditions for Poisson hail
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 315-353
- Print publication:
- March 2024
-
- Article
- Export citation
Normal and stable approximation to subgraph counts in superpositions of Bernoulli random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 401-419
- Print publication:
- June 2024
-
- Article
- Export citation
A systematic review of the evidence on the associations and safety of COVID-19 vaccination and post COVID-19 condition
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 18 August 2023, e145
-
- Article
-
- You have access
- Open access
- HTML
- Export citation