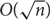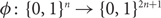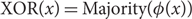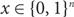Refine search
Actions for selected content:
52383 results in Statistics and Probability
Seroprevalence of pertussis in Madagascar and implications for vaccination
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 16 November 2020, e283
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lipschitz bijections between boolean functions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. 513-525
-
- Article
- Export citation
Factors associated with typical enteropathogenic Escherichia coli infection among children <5 years old with moderate-to-severe diarrhoea in rural western Kenya, 2008–2012
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 16 November 2020, e281
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A simple differential geometry for complex networks
-
- Journal:
- Network Science / Volume 9 / Issue S1 / October 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. S106-S133
-
- Article
- Export citation
Prevalence of asymptomatic COVID-19 infection using a seroepidemiological survey
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e300
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYTICAL RESULTS ON THE SERVICE PERFORMANCE OF STOCHASTIC CLEARING SYSTEMS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 13 November 2020, pp. 217-236
-
- Article
- Export citation
AVERAGE DERIVATIVE ESTIMATION UNDER MEASUREMENT ERROR
-
- Journal:
- Econometric Theory / Volume 37 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 1004-1033
-
- Article
- Export citation
Community movement and COVID-19: a global study using Google's Community Mobility Reports
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e284
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The insignificant structural break in the relationship between improved observed hand hygiene on methicillin-resistant Staphylococcus aureus bloodstream infection rates in Ireland: a data-driven re-analysis
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e297
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Development and validation of a simple risk score for diagnosing COVID-19 in the emergency room
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e273
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WHY DOES A HUMAN DIE? A STRUCTURAL APPROACH TO COHORT-WISE MORTALITY PREDICTION UNDER SURVIVAL ENERGY HYPOTHESIS
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 51 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 191-219
- Print publication:
- January 2021
-
- Article
-
- You have access
- Open access
- Export citation
Understanding the influence of the COVID-19 pandemic on hospital-based mortality in Burundi: a cross-sectional study comparing two time periods
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e280
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chasing the ghost of infection past: identifying thresholds of change during the COVID-19 infection in Spain
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e282
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A MEAN FIELD GAME ANALYSIS OF SIR DYNAMICS WITH VACCINATION
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 13 November 2020, pp. 482-499
-
- Article
- Export citation
The effect of a nighttime zoo event on spider monkey (Ateles geoffroyi) behavior
-
- Journal:
- Experimental Results / Volume 1 / 2020
- Published online by Cambridge University Press:
- 10 November 2020, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Making Kr+1-free graphs r-partite
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 10 November 2020, pp. 609-618
-
- Article
-
- You have access
- Open access
- Export citation
A spatial machine learning model for analysing customers’ lapse behaviour in life insurance
-
- Journal:
- Annals of Actuarial Science / Volume 15 / Issue 2 / July 2021
- Published online by Cambridge University Press:
- 10 November 2020, pp. 367-393
-
- Article
- Export citation
LIMIT THEOREMS FOR FACTOR MODELS
-
- Journal:
- Econometric Theory / Volume 37 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 1034-1074
-
- Article
- Export citation
A MULTIPLEX INTERDEPENDENT DURATIONS MODEL
-
- Journal:
- Econometric Theory / Volume 37 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 1238-1266
-
- Article
- Export citation
SUBGEOMETRICALLY ERGODIC AUTOREGRESSIONS
-
- Journal:
- Econometric Theory / Volume 38 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 09 November 2020, pp. 959-985
-
- Article
- Export citation