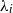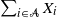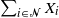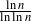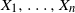Refine search
Actions for selected content:
52383 results in Statistics and Probability
AN EFFECTIVE BIAS-CORRECTED BAGGING METHOD FOR THE VALUATION OF LARGE VARIABLE ANNUITY PORTFOLIOS
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 50 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 08 September 2020, pp. 853-871
- Print publication:
- September 2020
-
- Article
- Export citation
Almost sure central limit theorems in stochastic geometry
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 705-734
- Print publication:
- September 2020
-
- Article
- Export citation
JPR volume 57 issue 3 Cover and Front matter
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. f1-f2
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
On branching models with alarm triggerings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 734-759
- Print publication:
- September 2020
-
- Article
- Export citation
Decorrelation of a class of Gibbs particle processes and asymptotic properties of U-statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 928-955
- Print publication:
- September 2020
-
- Article
- Export citation
Out-of-equilibrium random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 772-797
- Print publication:
- September 2020
-
- Article
- Export citation
Strong convergence of infinite color balanced urns under uniform ergodicity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 853-865
- Print publication:
- September 2020
-
- Article
- Export citation
APR volume 52 issue 3 Cover and Back matter
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. b1-b2
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
JPR volume 57 issue 3 Cover and Back matter
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. b1-b2
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Stochastically modeled weakly reversible reaction networks with a single linkage class
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 792-810
- Print publication:
- September 2020
-
- Article
- Export citation
Ergodicity of affine processes on the cone of symmetric positive semidefinite matrices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 825-854
- Print publication:
- September 2020
-
- Article
- Export citation
Trees grown under young-age preferential attachment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 911-927
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
TAXATION OF A GMWB VARIABLE ANNUITY IN A STOCHASTIC INTEREST RATE MODEL
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 50 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 02 September 2020, pp. 1001-1035
- Print publication:
- September 2020
-
- Article
- Export citation
Explicit results on conditional distributions of generalized exponential mixtures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 760-774
- Print publication:
- September 2020
-
- Article
- Export citation
Central limit theorems for coupled particle filters
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 942-1001
- Print publication:
- September 2020
-
- Article
- Export citation
Functional central limit theorems and moderate deviations for Poisson cluster processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 916-941
- Print publication:
- September 2020
-
- Article
- Export citation
Oscillations for order statistics of some discrete processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 703-719
- Print publication:
- September 2020
-
- Article
- Export citation
On moderate deviations in Poisson approximation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 1005-1027
- Print publication:
- September 2020
-
- Article
- Export citation
Stochastic comparisons of largest-order statistics for proportional reversed hazard rate model and applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 832-852
- Print publication:
- September 2020
-
- Article
- Export citation
Renewal in Hawkes processes with self-excitation and inhibition
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 879-915
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation