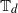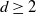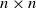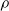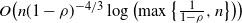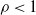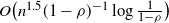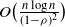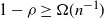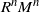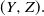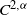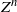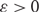Refine search
Actions for selected content:
52383 results in Statistics and Probability
On some threshold-one attractive interacting particle systems on homogeneous trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 866-898
- Print publication:
- September 2020
-
- Article
- Export citation
Improved queue-size scaling for input-queued switches via graph factorization
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 798-824
- Print publication:
- September 2020
-
- Article
- Export citation
Perron–Frobenius theory for kernels and Crump–Mode–Jagers processes with macro-individuals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 720-733
- Print publication:
- September 2020
-
- Article
- Export citation
Epidemiology of Enterotoxigenic Escherichia coli infection in Minnesota, 2016–2017
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 01 September 2020, e206
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cytogenomic results following high-chance non-invasive prenatal testing: a UK national audit
-
- Journal:
- Genetics Research / Volume 102 / 2020
- Published online by Cambridge University Press:
- 01 September 2020, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASB volume 50 issue 3 Cover and Front matter
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 50 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 22 September 2020, pp. f1-f2
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
JOINT OPTIMIZATION OF TRANSITION RULES AND THE PREMIUM SCALE IN A BONUS-MALUS SYSTEM
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 50 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 11 September 2020, pp. 743-776
- Print publication:
- September 2020
-
- Article
- Export citation
Mean square rate of convergence for random walk approximation of forward-backward SDEs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 735-771
- Print publication:
- September 2020
-
- Article
- Export citation
Flooding and diameter in general weighted random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 956-980
- Print publication:
- September 2020
-
- Article
- Export citation
Randomised rules for stopping problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 981-1004
- Print publication:
- September 2020
-
- Article
- Export citation

Essential Epidemiology
- An Introduction for Students and Health Professionals
-
- Published online:
- 31 August 2020
- Print publication:
- 29 November 2019
-
- Textbook
- Export citation
Dirac’s theorem for random regular graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 28 August 2020, pp. 17-36
-
- Article
- Export citation
COVID-19: public health management of the first two confirmed cases identified in the UK
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 28 August 2020, e194
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Resilience of the rank of random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 28 August 2020, pp. 163-174
-
- Article
- Export citation
Respiratory syncytial virus hospitalisations among young children: a data linkage study – Erratum
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 28 August 2020, e179
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stochastic approach to study control strategies of Covid-19 pandemic in India
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 28 August 2020, e200
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multisystem inflammatory syndrome associated with SARS-CoV-2 infection in 45 children: a first report from Iran
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 28 August 2020, e196
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Knowledge, attitudes and practices of healthcare workers during the early COVID-19 pandemic in a main, academic tertiary care centre in Saudi Arabia
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 28 August 2020, e203
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3 - Consistency of Finite Multivariate Markov Chains
- from Part One - Consistencies
-
- Book:
- Structured Dependence between Stochastic Processes
- Published online:
- 18 September 2020
- Print publication:
- 27 August 2020, pp 38-48
-
- Chapter
- Export citation
Appendix F - Martingale Problem: Some New Results Needed in this Book
- from Appendices
-
- Book:
- Structured Dependence between Stochastic Processes
- Published online:
- 18 September 2020
- Print publication:
- 27 August 2020, pp 250-254
-
- Chapter
- Export citation