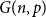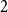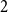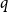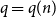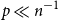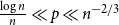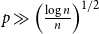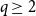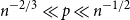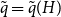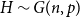Refine search
Actions for selected content:
52621 results in Statistics and Probability
Ramsey simplicity of random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 298-320
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exponential decay for constrained-degree percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 795-807
- Print publication:
- June 2025
-
- Article
- Export citation
Sufficient mathematical conditions for identical estimation of the liability for remaining coverage under the general measurement model and premium allocation approach
-
- Journal:
- British Actuarial Journal / Volume 29 / 2024
- Published online by Cambridge University Press:
- 03 December 2024, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Brownian range and the Brownian reversal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 775-794
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Individual claims reserving using the Aalen–Johansen estimator
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 55 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 29-49
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modeling mortality with Kernel Principal Component Analysis (KPCA) method
-
- Journal:
- Annals of Actuarial Science / Volume 18 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 03 December 2024, pp. 626-643
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Origin and evolution of West Nile virus lineage 1 in Italy
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hidden tail chains and recurrence equations for dependence parameters associated with extremes of stationary higher-order Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 407-452
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence of the derivative martingale for the branching random walk in time-inhomogeneous random environment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 642-676
- Print publication:
- June 2025
-
- Article
- Export citation
Gaussian fluctuations for the two-urn model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 607-641
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Delegated investment in retirement savings: is there value added?
-
- Journal:
- Annals of Actuarial Science / Volume 19 / Issue 2 / July 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 257-284
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inferring the proportion of undetected cholera infections from serological and clinical surveillance in an immunologically naive population
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e149
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Signalling and rich trustworthiness in data-driven healthcare: an interdisciplinary approach
- Part of
-
- Journal:
- Data & Policy / Volume 6 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Artificial intelligence at the bench: Legal and ethical challenges of informing—or misinforming—judicial decision-making through generative AI
- Part of
-
- Journal:
- Data & Policy / Volume 6 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gaussian approximation and moderate deviations of Poisson shot noises with application to compound generalized Hawkes processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 305-345
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Survival of the flattest in the quasispecies model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 566-606
- Print publication:
- June 2025
-
- Article
- Export citation
The ethics at the intersection of artificial intelligence and transhumanism: a personhood-based approach
- Part of
-
- Journal:
- Data & Policy / Volume 6 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Are we ready for the next anthrax outbreak? Lessons from a simulation exercise in a rural-based district in Uganda
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e151
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence speed and approximation accuracy of numerical MCMC
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 101-133
- Print publication:
- March 2025
-
- Article
- Export citation
An Augmented Variable Dirichlet Process mixture model for the analysis of dependent lifetimes
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 55 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 50-75
- Print publication:
- January 2025
-
- Article
- Export citation