Let 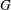 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G$ be a graph and
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G$ be a graph and  ${{\tau }}$ be an assignment of nonnegative thresholds to the vertices of
${{\tau }}$ be an assignment of nonnegative thresholds to the vertices of 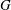 $G$. A subset of vertices,
$G$. A subset of vertices, 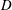 $D$, is an irreversible dynamic monopoly of
$D$, is an irreversible dynamic monopoly of  $(G, \tau )$ if the vertices of
$(G, \tau )$ if the vertices of 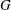 $G$ can be partitioned into subsets
$G$ can be partitioned into subsets 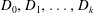 $D_0, D_1, \ldots, D_k$ such that
$D_0, D_1, \ldots, D_k$ such that 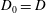 $D_0=D$ and, for all
$D_0=D$ and, for all 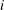 $i$ with
$i$ with 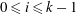 $0 \leq i \leq k-1$, each vertex
$0 \leq i \leq k-1$, each vertex  $v$ in
$v$ in 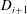 $D_{i+1}$ has at least
$D_{i+1}$ has at least 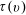 $\tau (v)$ neighbours in the union of
$\tau (v)$ neighbours in the union of 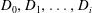 $D_0, D_1, \ldots, D_i$. Dynamic monopolies model the spread of influence or propagation of opinion in social networks, where the graph
$D_0, D_1, \ldots, D_i$. Dynamic monopolies model the spread of influence or propagation of opinion in social networks, where the graph 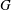 $G$ represents the underlying network. The smallest cardinality of any dynamic monopoly of
$G$ represents the underlying network. The smallest cardinality of any dynamic monopoly of 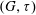 $(G,\tau )$ is denoted by
$(G,\tau )$ is denoted by 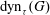 $\mathrm{dyn}_{\tau }(G)$. In this paper we assume that the threshold of each vertex
$\mathrm{dyn}_{\tau }(G)$. In this paper we assume that the threshold of each vertex  $v$ of the network is a random variable
$v$ of the network is a random variable 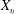 $X_v$ such that
$X_v$ such that  $0\leq X_v \leq \deg _G(v)+1$. We obtain sharp bounds on the expectation and the concentration of
$0\leq X_v \leq \deg _G(v)+1$. We obtain sharp bounds on the expectation and the concentration of 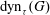 $\mathrm{dyn}_{\tau }(G)$ around its mean value. We also obtain some lower bounds for the size of dynamic monopolies in terms of the order of graph and expectation of the thresholds.
$\mathrm{dyn}_{\tau }(G)$ around its mean value. We also obtain some lower bounds for the size of dynamic monopolies in terms of the order of graph and expectation of the thresholds.
 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}30p$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}30p$