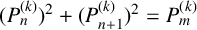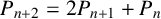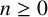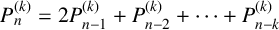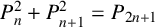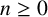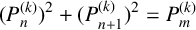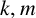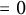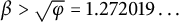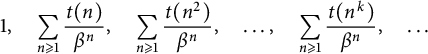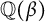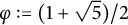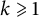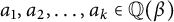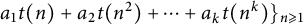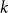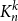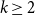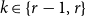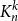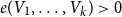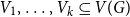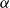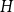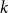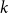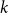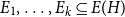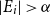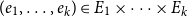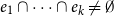Refine listing
Actions for selected content:
1418489 results in Open Access
The future of neuroscience in developmental psychopathology
-
- Journal:
- Development and Psychopathology / Volume 36 / Issue 5 / December 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 2149-2164
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DIOPHANTINE EQUATION
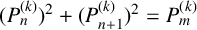 $(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
$(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 211-215
- Print publication:
- October 2024
-
- Article
- Export citation
Mitigating the effects of water-deficit stress on potato growth and photosynthesis using mycorrhizal fungi and phosphate-solubilizing bacteria
-
- Journal:
- The Journal of Agricultural Science / Volume 162 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 46-58
-
- Article
- Export citation
Manipulation in politics and public policy
-
- Journal:
- Economics & Philosophy / Volume 40 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 685-710
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Donald Harman Akenson, The Americanization of the Apocalypse: Creating America's Own Bible (Oxford: OUP, 2023), pp. xv + 501. $137.00
-
- Journal:
- Scottish Journal of Theology / Volume 77 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 192-193
- Print publication:
- May 2024
-
- Article
- Export citation
Efficacy of commercially available entomopathogenic nematodes against insect pests of canola in Alberta, Canada
-
- Journal:
- Journal of Helminthology / Volume 98 / 2024
- Published online by Cambridge University Press:
- 06 March 2024, e21
-
- Article
- Export citation
Hegel contra Hegel: Eurocentrism, Colonialism, and Progress
-
- Journal:
- Hegel Bulletin / Volume 45 / Issue 2 / August 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 237-264
- Print publication:
- August 2024
-
- Article
- Export citation
Removal of central venous catheter using Evolution® Rotating Dilator
-
- Journal:
- Cardiology in the Young / Volume 34 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1142-1144
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear independence of series related to the Thue–Morse sequence along powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 822-832
- Print publication:
- September 2024
-
- Article
- Export citation
Susanne Mühleisen , Genre in World Englishes: Case studies from the Caribbean (Varieties of English Around the World, G67). Amsterdam and Philadelphia: John Benjamins, 2022. Pp. viii + 229. ISBN 9789027211385.
-
- Journal:
- English Language & Linguistics / Volume 28 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 798-802
-
- Article
- Export citation
Credence and Belief: Distance- and Utility-Based Approaches
-
- Journal:
- Philosophy of Science / Volume 91 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 759-779
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Creating a flow restrictor in ductal stenting: a novel technique
-
- Journal:
- Cardiology in the Young / Volume 34 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1159-1160
-
- Article
- Export citation
DrSaheed Aderinto. Animality and Colonial Subjecthood in Africa: The Human and Nonhuman Creatures of Nigeria. Athens, OH: Ohio University Press, 2022. 340 pp. Photographs. Tables. Notes. Bibliography. Index. $36.95. Paper. ISBN: 9780821424766.
-
- Journal:
- African Studies Review / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 520-521
-
- Article
-
- You have access
- HTML
- Export citation
Effects of beef fat enriched with trans vaccenic acid and cis9, trans11-CLA on glucose homoeostasis and hepatic lipid accumulation in high-fat diet-induced obese mice
-
- Journal:
- British Journal of Nutrition / Volume 131 / Issue 12 / 28 June 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1975-1984
- Print publication:
- 28 June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Professor William Philip Trehearne James, FRSE FMedSci CBE (1938–2023)
-
- Journal:
- British Journal of Nutrition / Volume 131 / Issue 10 / 28 May 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1774-1776
- Print publication:
- 28 May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Alison E. Arnold and Jonathan C. Kramer. What in the World is Music? Second Edition. New York: Routledge, 2023. viii, 467 pp., list of figures, list of maps, glossary, further resources, media index, index. ISBN 9781032341491 (print) and ISBN 9781032432847 (e-book).
-
- Journal:
- Yearbook for Traditional Music / Volume 56 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 116-119
- Print publication:
- July 2024
-
- Article
- Export citation
Large monochromatic components in expansive hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 467-483
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Velocity gradient analysis of a head-on vortex ring collision
-
- Journal:
- Journal of Fluid Mechanics / Volume 982 / 10 March 2024
- Published online by Cambridge University Press:
- 05 March 2024, A16
-
- Article
- Export citation
Listening in on the Neighbors: The Reception of German and Austrian Radio in Cold War Czechoslovakia – CORRIGENDUM
-
- Journal:
- Central European History / Volume 57 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 05 March 2024, p. 308
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tracial weights on topological graph algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 3428-3454
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation