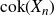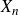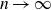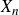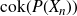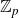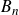Refine listing
Actions for selected content:
1416829 results in Open Access
A new epiphytic species of Gyalolechia with a maritime, Mediterranean-Macaronesian distribution
-
- Journal:
- The Lichenologist / Volume 57 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 53-60
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revolts and Political Violence in Early Modern Imagery. Malte Griesse, Monika Barget, and David de Boer, eds. Brill’s Studies on Art, Art History, and Intellectual History 54. Leiden: Brill, 2021. xvi + 324 pp. $119.
-
- Journal:
- Renaissance Quarterly / Volume 78 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 18 June 2025, pp. 212-214
- Print publication:
- Spring 2025
-
- Article
- Export citation
Christian Images and Their Jewish Desecrators: The History of an Allegation, 400–1700. Katherine Aron-Beller. Jewish Culture and Contexts. Philadelphia: University of Pennsylvania Press, 2024. xii + 426 pp. $79.95.
-
- Journal:
- Renaissance Quarterly / Volume 78 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 18 June 2025, pp. 191-193
- Print publication:
- Spring 2025
-
- Article
- Export citation
Research Handbook on Asylum and Refugee Policy. Jane Freedman and Glenda Santana de Andrade, eds. Cheltenham, UK: Edward Elgar, 2024. 390 pp. ISBN: 978-1-80220-458-2. US$280.00.
-
- Journal:
- International Journal of Legal Information / Volume 53 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 22 April 2025, p. 80
- Print publication:
- Spring 2025
-
- Article
- Export citation
Response to Malte Frøslee Ibsen’s Review of The Militant Intellect: Critical Theory’s Conceptual Personae
-
- Journal:
- Perspectives on Politics / Volume 23 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 20 March 2025, pp. 325-326
- Print publication:
- March 2025
-
- Article
- Export citation
The cokernel of a polynomial push-forward of a random integral matrix with concentrated residue
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 229-257
- Print publication:
- March 2025
-
- Article
- Export citation
The EU Reexamined: A Governance Model in Transition. Jorn Axel Kammerer, Hans-Bernd Schafer, and Kaushik Basu, eds. Cheltenham, UK; Northampton, MA: Edward Elgar, 2024. 327 pp. ISBN: 978-1-0353-1485-0. US$175.00.
-
- Journal:
- International Journal of Legal Information / Volume 53 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 21 March 2025, p. 79
- Print publication:
- Spring 2025
-
- Article
- Export citation
JEH volume 85 issue 1 Cover and Front matter
-
- Journal:
- The Journal of Economic History / Volume 85 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 04 March 2025, pp. f1-f4
- Print publication:
- March 2025
-
- Article
-
- You have access
- Export citation
NBF volume 106 issue 2 Cover and Back matter
-
- Journal:
- New Blackfriars / Volume 106 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 05 March 2025, p. b1
- Print publication:
- March 2025
-
- Article
-
- You have access
- Export citation
Reflections on Global Health Law in the COVID-19 Response
-
- Journal:
- Journal of Law, Medicine & Ethics / Volume 53 / Issue S1 / Spring 2025
- Published online by Cambridge University Press:
- 14 April 2025, p. 46
- Print publication:
- Spring 2025
-
- Article
- Export citation
Victoria Harms. The Making of Dissidents: Hungary’s Democratic Opposition and Its Western Friends, 1973–1998. Pittsburgh: University of Pittsburgh Press, 2024. x, 410 pp. Notes. Bibliography. Index. Photographs. Tables. $60.00, hard bound.
-
- Journal:
- Slavic Review / Volume 84 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 185-186
- Print publication:
- Spring 2025
-
- Article
- Export citation
Martin Luther and the Arts: Music, Images, and Drama to Promote the Reformation. Andreas Loewe and Katherine Firth. Studies in Medieval and Reformation Traditions 236. Leiden: Brill, 2023. xiv + 281 pp. $139.
-
- Journal:
- Renaissance Quarterly / Volume 78 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 18 June 2025, pp. 278-279
- Print publication:
- Spring 2025
-
- Article
- Export citation
Common graphs with arbitrary chromatic number
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 03 July 2025, pp. 594-634
- Print publication:
- March 2025
-
- Article
- Export citation
Purulia Chhou: Tradition, Transformation, and Contemporary Trends
-
- Journal:
- TDR: The Drama Review / Volume 69 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 132-152
- Print publication:
- March 2025
-
- Article
- Export citation
Smartphone apps for overweight and obesity: current evidence in a fast-moving field
- Part of
-
- Journal:
- BJPsych Advances / Volume 31 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 09 April 2025, pp. 68-72
- Print publication:
- March 2025
-
- Article
- Export citation
Negotiating Medicare Drug Prices: A New Attempt to Control Purchase Prices
-
- Journal:
- Journal of Law, Medicine & Ethics / Volume 53 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 147-157
- Print publication:
- Spring 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poètiques de l’amour: Sexualité, genre, pouvoir XIe–XVe siècle. Joël Blanchard. Paris: Passés/Composés, 2022. 334 pp. €22.
-
- Journal:
- Renaissance Quarterly / Volume 78 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 18 June 2025, pp. 320-322
- Print publication:
- Spring 2025
-
- Article
- Export citation
ASSOCIATION FOR SYMBOLIC LOGIC
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 16 April 2025, pp. 188-193
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
IS CODE DESTINED TO SUPERSEDE LAW? BEHAVIOURAL CONTROL BY CODE AND LEGAL THEORY
-
- Journal:
- The Cambridge Law Journal / Volume 84 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 06 March 2025, pp. 175-208
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Courtly Mediators: Transcultural Objects between Renaissance Italy and the Islamic World. Leah R. Clark. Cambridge: Cambridge University Press, 2023. xx + 336 pp. $130.
-
- Journal:
- Renaissance Quarterly / Volume 78 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 18 June 2025, pp. 193-194
- Print publication:
- Spring 2025
-
- Article
- Export citation