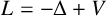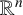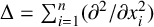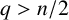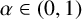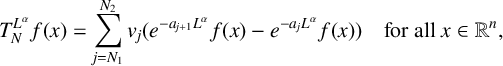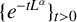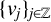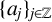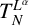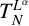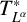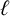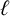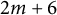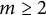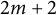Refine listing
Actions for selected content:
1417854 results in Open Access
A pore-scale resolved direct numerical simulation study for scaling analysis of the solutal convection in porous media
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A21
-
- Article
- Export citation
BOUNDEDNESS OF DIFFERENTIAL TRANSFORMS FOR FRACTIONAL HEAT SEMIGROUPS GENERATED BY SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 210-244
- Print publication:
- April 2025
-
- Article
- Export citation
Random growth via gradient flow aggregation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 735-755
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Instability evolution on a shock-accelerated cylindrical fluid layer with arbitrary Atwood numbers
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A9
-
- Article
- Export citation
Uniqueness theorems for meromorphic inner functions and canonical systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 124-140
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Identification of cross-frequency interactions in compressible cavity flow using harmonic resolvent analysis
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Navigating Diphtheria Resurgence in Pakistan’s Conflict-Ridden and Disaster-Prone Area
-
- Journal:
- Disaster Medicine and Public Health Preparedness / Volume 18 / 2024
- Published online by Cambridge University Press:
- 25 November 2024, e288
-
- Article
- Export citation
Disease Burden in the Context of Disasters: Insights from Over 6.7 million Respondents in the Bangladesh Disaster-Related Statistics of 2021
-
- Journal:
- Disaster Medicine and Public Health Preparedness / Volume 18 / 2024
- Published online by Cambridge University Press:
- 25 November 2024, e283
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Governance by One-Lot Shares
-
- Journal:
- Journal of Financial and Quantitative Analysis / Volume 60 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 874-909
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- Export citation
Turbulence statistics and structures in fully developed open channel flows with periodic surface coverages
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the theory of body motion in confined Stokesian fluids
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JEH volume 84 issue 4 Cover and Back matter
-
- Journal:
- The Journal of Economic History / Volume 84 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. b1-b3
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation
Commutativity properties of Quinn spectra
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1848-1936
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eye-tracking analysis to assess the mental load of unmanned aerial system operators: systematic review and future directions
-
- Journal:
- The Aeronautical Journal / Volume 129 / Issue 1333 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 529-558
-
- Article
- Export citation
The Art of Disruption: Decolonial Potentiality in Fatou Cissé’s La ville en mouv’ment
-
- Journal:
- African Studies Review / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. 568-589
-
- Article
- Export citation
EXTENDING CONGRUENCES FOR OVERPARTITIONS WITH
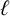 $\ell $-REGULAR NONOVERLINED PARTS
$\ell $-REGULAR NONOVERLINED PARTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 478-489
- Print publication:
- June 2025
-
- Article
- Export citation
Editors’ Notes
-
- Journal:
- The Journal of Economic History / Volume 84 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1240-1243
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Poncelet’s closure theorem and the embedded topology of conic-line arrangements
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 109-123
- Print publication:
- March 2025
-
- Article
- Export citation
Constantine Christos Vassiliou: Moderate Liberalism and the Scottish Enlightenment: Montesquieu, Hume, Smith and Ferguson. (Edinburgh: Edinburgh University Press, 2023. Pp. xvi, 203.)
-
- Journal:
- The Review of Politics / Volume 86 / Issue 4 / Fall 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. 570-572
-
- Article
- Export citation