Refine search
Actions for selected content:
37 results
Atypical bifurcation for periodic solutions of ϕ-Laplacian systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-27
-
- Article
- Export citation
Multiple solutions to relativistic systems with potential boundary conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-14
-
- Article
- Export citation
Asymptotic formulas of the eigenvalues for the linearization of the scalar field equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 307-344
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A modelling framework for efficient reduced order simulations of parametrised lithium-ion battery cells
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 554-591
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLUTIONS TO DIFFERENTIAL EQUATIONS VIA FIXED POINT APPROACHES: NEW MATHEMATICAL FOUNDATIONS AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 163-164
- Print publication:
- August 2022
-
- Article
-
- You have access
- HTML
- Export citation
Periodic solutions of p-Laplacian differential equations with jumping nonlinearity across half-eigenvalues
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 07 January 2022, pp. 307-326
- Print publication:
- February 2023
-
- Article
- Export citation
The maximal current carried by a normal–superconducting interface in the absence of magnetic field
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 27 August 2019, pp. 544-552
-
- Article
- Export citation
APPLICATION OF PROJECTION ALGORITHMS TO DIFFERENTIAL EQUATIONS: BOUNDARY VALUE PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 23-46
-
- Article
-
- You have access
- Export citation
A generalization of Krasnosel'skii compression fixed point theorem by using star convex sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 25 January 2019, pp. 277-303
- Print publication:
- February 2020
-
- Article
- Export citation
Pairs of positive periodic solutions of nonlinear ODEs with indefinite weight: a topological degree approach for the super–sublinear case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 449-474
- Print publication:
- June 2016
-
- Article
- Export citation
Boundary-Value Problems for Third-Order Lipschitz Ordinary Differential Equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 28 October 2014, pp. 183-197
-
- Article
-
- You have access
- Export citation
On Nonlinear Boundary Conditions Involving Decomposable Linear Functionals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 421-439
-
- Article
-
- You have access
- Export citation
A VARIATIONAL APPROACH FOR ONE-DIMENSIONAL PRESCRIBED MEAN CURVATURE PROBLEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 145-161
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
STRICTLY POSITIVE SOLUTIONS FOR ONE-DIMENSIONAL NONLINEAR PROBLEMS INVOLVING THE
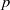 $p$-LAPLACIAN
$p$-LAPLACIAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 06 September 2013, pp. 243-251
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
Solutions and multiple solutions for superlinear perturbations of the periodic scalar p-Laplacian
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 805-827
-
- Article
-
- You have access
- Export citation
NONTRIVIAL SOLUTIONS FOR STURM–LIOUVILLE SYSTEMS VIA A LOCAL MINIMUM THEOREM FOR FUNCTIONALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 8-18
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
IMPULSIVE PERIODIC SOLUTIONS FOR SINGULAR PROBLEMS VIA VARIATIONAL METHODS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 193-204
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
EXPLICIT SERIES SOLUTION OF A CLOSURE MODEL FOR THE VON KÁRMÁN–HOWARTH EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 05 September 2011, pp. 179-202
-
- Article
-
- You have access
- Export citation
AN EXISTENCE RESULT OF ONE NONTRIVIAL SOLUTION FOR TWO POINT BOUNDARY VALUE PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 13 July 2011, pp. 288-299
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
Higher-order singular multi-point boundary-value problems on time scales
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 345-361
-
- Article
-
- You have access
- Export citation












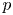
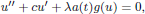
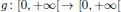 is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when
is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when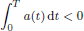
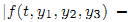
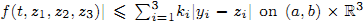 , questions involving ‘uniqueness implies uniqueness’, ‘uniqueness implies existence’ and ‘optimal length subintervals of (
, questions involving ‘uniqueness implies uniqueness’, ‘uniqueness implies existence’ and ‘optimal length subintervals of (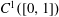
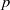
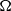
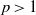
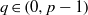
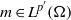
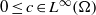
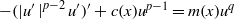
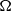
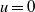
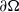
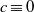

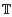 with a positive parameter λ in the differential equations. A homeomorphism and homomorphism ø are involved both in the differential equation and in the boundary conditions. Criteria are obtained for the existence and uniqueness of positive solutions. The dependence of positive solutions on the parameter λ is studied. Applications of our results to special problems are also discussed. Our analysis mainly relies on the mixed monotone operator theory. The results here are new, even in the cases of second-order differential and difference equations.
with a positive parameter λ in the differential equations. A homeomorphism and homomorphism ø are involved both in the differential equation and in the boundary conditions. Criteria are obtained for the existence and uniqueness of positive solutions. The dependence of positive solutions on the parameter λ is studied. Applications of our results to special problems are also discussed. Our analysis mainly relies on the mixed monotone operator theory. The results here are new, even in the cases of second-order differential and difference equations.