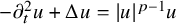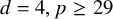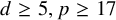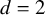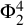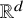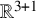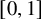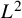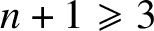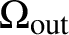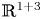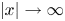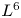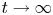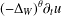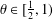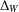Refine search
Actions for selected content:
9 results
On blow-up for the supercritical defocusing nonlinear wave equation
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 31 March 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global dynamics for the stochastic nonlinear beam equations on the four-dimensional torus
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A remark on Gibbs measures with log-correlated Gaussian fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The zero mass problem for Klein-Gordon equations: quadratic null interactions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 20 May 2022, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inverse problems for nonlinear hyperbolic equations with disjoint sources and receivers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 02 November 2021, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scattering for critical wave equations with variable coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 298-316
-
- Article
- Export citation
Invariant Gibbs dynamics for the dynamical sine-Gordon model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 16 September 2020, pp. 1450-1466
- Print publication:
- October 2021
-
- Article
- Export citation
Existence of multiple periodic solutions to a semilinear wave equation with x-dependent coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 04 June 2019, pp. 2586-2606
- Print publication:
- October 2020
-
- Article
- Export citation
GLOBAL EXISTENCE OF WEAK SOLUTIONS FOR STRONGLY DAMPED WAVE EQUATIONS WITH NONLINEAR BOUNDARY CONDITIONS AND BALANCED POTENTIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 432-444
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation