Refine search
Actions for selected content:
23 results
MORPHISMS OF CUNTZ–PIMSNER ALGEBRAS FROM COMPLETELY POSITIVE MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 31 October 2025, pp. 1-40
-
- Article
- Export citation
ON TOEPLITZ ALGEBRAS OF PRODUCT SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Fock covariance for product systems and the reduced Hao–Ng isomorphism problem by discrete actions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-53
-
- Article
- Export citation
Isometric dilations for representations of product systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Picard groups of inclusions of
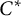 $C^*$-algebras induced by equivalence bimodules
$C^*$-algebras induced by equivalence bimodules
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 743-758
- Print publication:
- September 2022
-
- Article
- Export citation
Operator equalities and Characterizations of Orthogonality in Pre-Hilbert C*-Modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 17 June 2021, pp. 594-614
-
- Article
- Export citation
Classification of irreversible and reversible Pimsner operator algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 13 January 2021, pp. 2510-2535
- Print publication:
- December 2020
-
- Article
- Export citation
Dimension groups for self-similar maps and matrix representations of the cores of the associated C*-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 12 May 2020, pp. 1013-1056
- Print publication:
- August 2021
-
- Article
- Export citation
Finite-dimensional approximations for Nica–Pimsner algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 3375-3402
- Print publication:
- December 2020
-
- Article
- Export citation
Rigid C*-Tensor Categories and their Realizations as Hilbert C*-Bimodules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 367-393
-
- Article
- Export citation
Subgroup Correspondences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 14 August 2018, pp. 1127-1154
-
- Article
- Export citation
FRAME-LESS HILBERT C*-MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 07 February 2018, pp. 25-31
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
A stabilization theorem for Fell bundles over groupoids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 79-100
- Print publication:
- February 2018
-
- Article
- Export citation
The Inner Corona Algebra of a C 0(X)-Algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 299-318
-
- Article
- Export citation
FRAMES IN HILBERT C*-MODULES AND MORITA EQUIVALENT C*-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 03 August 2016, pp. 1-10
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
ADJOINT FUNCTORS BETWEEN CATEGORIES OF HILBERT
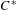 $C^{\ast }$ -MODULES
$C^{\ast }$ -MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 30 June 2016, pp. 453-488
- Print publication:
- April 2018
-
- Article
- Export citation
Parabolic induction and restriction via
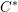 $C^{\ast }$-algebras and Hilbert
$C^{\ast }$-algebras and Hilbert 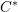 $C^{\ast }$-modules
$C^{\ast }$-modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 1286-1318
- Print publication:
- June 2016
-
- Article
- Export citation
OBSTRUCTIONS TO A GENERAL CHARACTERIZATION OF GRAPH CORRESPONDENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 169-188
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
On derivations and elementary operators on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 515-534
-
- Article
-
- You have access
- Export citation
SOME C*-ALGEBRAS ASSOCIATED TO QUANTUM GAUGE THEORIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 18 May 2011, pp. 9-24
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation






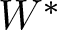
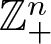
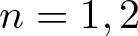
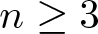
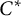
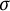
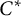
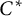
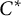
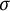
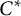
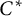
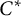
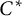
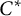
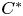
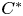
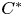
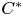
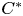
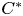
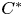
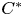
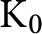
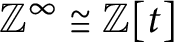
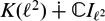
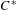
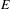
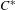

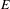
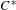
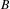
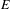
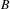

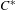
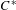
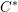
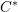
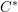
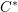
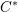
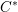
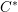
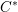

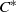
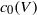
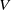
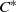
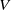
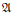 over the maximal ideal space of the centre of
over the maximal ideal space of the centre of 