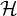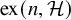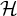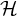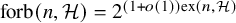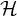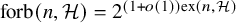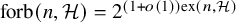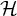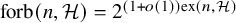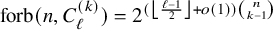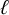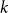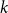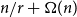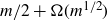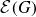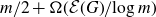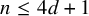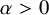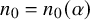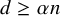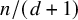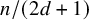Refine search
Actions for selected content:
138 results
On the number of
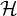 $\mathcal {H}$-free hypergraphs
$\mathcal {H}$-free hypergraphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 14 / 2026
- Published online by Cambridge University Press:
- 09 February 2026, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hypergraphs without complete partite subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 11 December 2025, pp. 1-4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PSEUDOFINITENESS AND MEASURABILITY OF THE EVERYWHERE INFINITE FOREST
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A rainbow Dirac theorem for loose Hamilton cycles in hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-29
-
- Article
- Export citation
Graph operations and a unified method for Turán-type problems on paths, cycles, and matchings
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-27
-
- Article
- Export citation
Powers of Hamilton cycles in oriented and directed graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 28 October 2025, pp. 101-133
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Disperse hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 27 October 2025, pp. 89-100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the computational complexity of weak saturation
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 16 October 2025, pp. 83-88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inducibility of rainbow graphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 02 October 2025, pp. 191-218
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On extremal numbers of the triangle plus the four-cycle
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 23 September 2025, e154
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the multicolor Turán conjecture for color-critical graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-31
-
- Article
- Export citation
Embedding nearly spanning trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 11 August 2025, pp. 927-931
-
- Article
- Export citation
A stability theorem for multi-partite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 11 August 2025, pp. 821-847
-
- Article
- Export citation
A conditional lower bound for the Turán number of spheres
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 11 August 2025, pp. 848-856
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Common pairs of graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 649-670
-
- Article
- Export citation
Tight Hamilton cycles with high discrepancy
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 30 May 2025, pp. 565-584
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Short proof of the hypergraph container theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 16 May 2025, pp. 621-624
-
- Article
- Export citation
Large cuts in hypergraphs via energy
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 45-61
- Print publication:
- July 2025
-
- Article
- Export citation
Hypergraph removal with polynomial bounds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 321-330
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cycle Partitions in Dense Regular Digraphs and Oriented Graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation