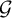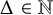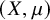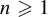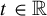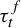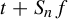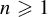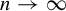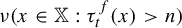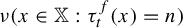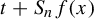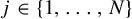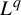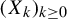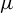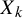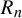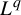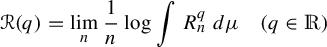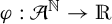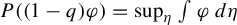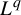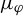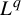Refine search
Actions for selected content:
42 results
ON THE SHORTEST DISTANCE BETWEEN ORBITS IN CONFORMAL ITERATED FUNCTION SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-11
-
- Article
- Export citation
Large deviations for occupation and waiting times of infinite ergodic transformations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit theorems for a class of unbounded observables with an application to ‘Sampling the Lindelöf hypothesis’
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 12 August 2025, pp. 34-92
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable functional CLT for deterministic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 26 May 2025, pp. 3192-3222
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measurable Vizing’s theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A parameter ASIP for the quadratic family
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 24 September 2024, pp. 663-703
- Print publication:
- March 2025
-
- Article
- Export citation
Rigidity of pressures of Hölder potentials and the fitting of analytic functions through them
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 18 March 2024, pp. 3530-3564
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable laws for random dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 3041-3090
- Print publication:
- November 2024
-
- Article
- Export citation
Approximation with ergodic processes and testability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 23 January 2024, pp. 1040-1059
- Print publication:
- September 2024
-
- Article
- Export citation
Invariant measures for substitutions on countable alphabets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2533-2564
- Print publication:
- September 2024
-
- Article
- Export citation
A nonconservative kinetic framework under the action of an external force field: Theoretical results with application inspired to ecology
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 1170-1186
-
- Article
- Export citation
Orbits closeness for slowly mixing dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1192-1208
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wasserstein convergence rates in the invariance principle for deterministic dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 1172-1191
- Print publication:
- April 2024
-
- Article
- Export citation
Counting independent sets in amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 May 2023, pp. 958-1012
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conditioned limit theorems for hyperbolic dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 50-117
- Print publication:
- January 2024
-
- Article
- Export citation
A factor of i.i.d. with uniform marginals and infinite clusters spanned by equal labels
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 22 December 2022, pp. 3707-3725
- Print publication:
- November 2023
-
- Article
- Export citation
Mixing and rigidity along asymptotically linearly independent sequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 3506-3537
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quenched and annealed equilibrium states for random Ruelle expanding maps and applications
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 09 September 2022, pp. 3150-3192
- Print publication:
- September 2023
-
- Article
- Export citation
Return-time
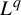 $L^q$-spectrum for equilibrium states with potentials of summable variation
$L^q$-spectrum for equilibrium states with potentials of summable variation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 2489-2515
- Print publication:
- August 2023
-
- Article
- Export citation
A non-singular version of the Oseledeč ergodic theorem
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 24 February 2022, pp. 873-886
- Print publication:
- March 2023
-
- Article
- Export citation