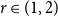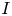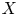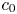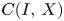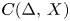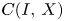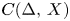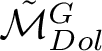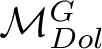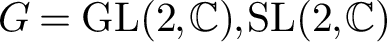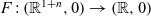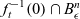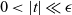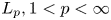Refine search
Actions for selected content:
25847 results in Abstract analysis
References
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp 456-479
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp i-iv
-
- Chapter
- Export citation
3 - Numerical Contraction
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp 97-145
-
- Chapter
- Export citation
5 - Numerical Range and Dilation
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp 194-240
-
- Chapter
- Export citation
6 - Numerical Range of Finite Matrix
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp 241-293
-
- Chapter
- Export citation
2 - Numerical Ranges of Special Operators
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp 51-96
-
- Chapter
- Export citation
1 - Numerical Range
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp 11-50
-
- Chapter
- Export citation
7 - Numerical Range of Sn-Matrix
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp 294-357
-
- Chapter
- Export citation
List of Symbols
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp xiii--xviii
-
- Chapter
- Export citation
Appendix - Convex Set
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp 446-455
-
- Chapter
- Export citation
Contents
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp vii-viii
-
- Chapter
- Export citation
Preface
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp ix-xii
-
- Chapter
- Export citation
Dedication
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp v-vi
-
- Chapter
- Export citation
4 - Algebraic and Essential Numerical Ranges
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp 146-193
-
- Chapter
- Export citation
Index
-
- Book:
- Numerical Ranges of Hilbert Space Operators
- Published online:
- 27 July 2021
- Print publication:
- 05 August 2021, pp 480-484
-
- Chapter
- Export citation
On Turán exponents of bipartite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 04 August 2021, pp. 333-344
-
- Article
- Export citation
An example regarding Kalton's paper ‘isomorphisms between spaces of vector-valued continuous functions’
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 02 August 2021, pp. 615-619
-
- Article
- Export citation
INTERSECTION COHOMOLOGY OF THE MODULI SPACE OF HIGGS BUNDLES ON A GENUS 2 CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 02 August 2021, pp. 1037-1086
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TOPOLOGY OF 1-PARAMETER DEFORMATIONS OF NON-ISOLATED REAL SINGULARITIES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 30 July 2021, pp. 484-498
-
- Article
- Export citation
Spectral properties of a beam equation with eigenvalue parameter occurring linearly in the boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 30 July 2021, pp. 780-801
- Print publication:
- June 2022
-
- Article
- Export citation