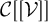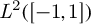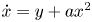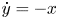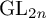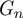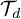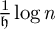Refine search
Actions for selected content:
25847 results in Abstract analysis
Index
-
- Book:
- Singularly Perturbed Methods for Nonlinear Elliptic Problems
- Published online:
- 28 January 2021
- Print publication:
- 18 February 2021, pp 251-252
-
- Chapter
- Export citation
1 - Non-compact Elliptic Problems
-
- Book:
- Singularly Perturbed Methods for Nonlinear Elliptic Problems
- Published online:
- 28 January 2021
- Print publication:
- 18 February 2021, pp 1-53
-
- Chapter
- Export citation
Contents
-
- Book:
- Singularly Perturbed Methods for Nonlinear Elliptic Problems
- Published online:
- 28 January 2021
- Print publication:
- 18 February 2021, pp v-vi
-
- Chapter
- Export citation
3 - Local Uniqueness of Solutions
-
- Book:
- Singularly Perturbed Methods for Nonlinear Elliptic Problems
- Published online:
- 28 January 2021
- Print publication:
- 18 February 2021, pp 129-155
-
- Chapter
- Export citation
Preface
-
- Book:
- Singularly Perturbed Methods for Nonlinear Elliptic Problems
- Published online:
- 28 January 2021
- Print publication:
- 18 February 2021, pp vii-x
-
- Chapter
- Export citation
References
-
- Book:
- Singularly Perturbed Methods for Nonlinear Elliptic Problems
- Published online:
- 28 January 2021
- Print publication:
- 18 February 2021, pp 242-250
-
- Chapter
- Export citation
Existence of solution for elliptic equations with supercritical Trudinger–Moser growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 16 February 2021, pp. 291-310
- Print publication:
- April 2022
-
- Article
- Export citation
Identifiability of stochastically modelled reaction networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 865-887
-
- Article
- Export citation
PERIODS OF DRINFELD MODULES AND LOCAL SHTUKAS WITH COMPLEX MULTIPLICATION – ERRATUM
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 12 February 2021, pp. 2247-2251
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
On the first eigenvalue of the Laplace operator for compact spacelike submanifolds in Lorentz–Minkowski spacetime 𝕃m
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 311-330
- Print publication:
- April 2022
-
- Article
- Export citation
THE METRIC PROJECTIONS ONTO CLOSED CONVEX CONES IN A HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 1617-1650
- Print publication:
- September 2022
-
- Article
- Export citation
The cyclicity of the period annulus of a reversible quadratic system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 10 February 2021, pp. 281-290
- Print publication:
- April 2022
-
- Article
- Export citation
RAISING THE LEVEL OF AUTOMORPHIC REPRESENTATIONS OF
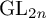 $\mathrm {GL}_{2n}$ OF UNITARY TYPE
$\mathrm {GL}_{2n}$ OF UNITARY TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 1421-1444
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
CUTOFF AT THE ENTROPIC TIME FOR RANDOM WALKS ON COVERED EXPANDER GRAPHS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 1571-1616
- Print publication:
- September 2022
-
- Article
- Export citation
RANDOM REAL BRANCHED COVERINGS OF THE PROJECTIVE LINE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 1783-1799
- Print publication:
- September 2022
-
- Article
- Export citation
Homotopy of gauge groups over high-dimensional manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 February 2021, pp. 182-208
- Print publication:
- February 2022
-
- Article
- Export citation
Modelling, computation and analysis on combustion of explosives
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 February 2021, pp. 27-57
-
- Article
- Export citation
INVERSE OF FREQUENTLY HYPERCYCLIC OPERATORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 04 February 2021, pp. 1867-1886
- Print publication:
- November 2022
-
- Article
- Export citation
COMPLETELY PRIME ONE-SIDED IDEALS IN SKEW POLYNOMIAL RINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 03 February 2021, pp. 114-121
-
- Article
- Export citation
KODAIRA DIMENSION OF UNIVERSAL HOLOMORPHIC SYMPLECTIC VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 1849-1866
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation