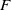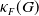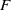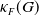Refine search
Actions for selected content:
25814 results in Abstract analysis
On perfect subdivision tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 421-444
-
- Article
- Export citation
Kostant’s problem for parabolic Verma modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 594-615
-
- Article
- Export citation
A stability inequality for planar lens partition
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ALGEBRAIC CLASSES IN MIXED CHARACTERISTIC AND ANDRÉ’S p-ADIC PERIODS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1093-1138
- Print publication:
- July 2025
-
- Article
- Export citation
Strongly dense representations of surface groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 583-593
-
- Article
- Export citation
Models for information propagation on graphs
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 1040-1061
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Irreducible factors of a polynomial
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 573-582
-
- Article
- Export citation
Optimal linear sofic approximations of countable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 245-268
- Print publication:
- May 2025
-
- Article
- Export citation
12 - Continuity and Coincidence Theorems
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp 184-202
-
- Chapter
- Export citation
Conditions for the supersolvability of
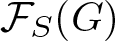 $\mathcal{F}_{S}(G)$
$\mathcal{F}_{S}(G)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 23 January 2025, pp. 566-572
-
- Article
- Export citation
13 - * Non-separable Variants
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp 203-221
-
- Chapter
- Export citation
2 - Baire Category and Related Results
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp 34-50
-
- Chapter
- Export citation
Preface
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp xi-xiv
-
- Chapter
- Export citation
Index
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp 324-332
-
- Chapter
- Export citation
Dedication
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp v-vi
-
- Chapter
- Export citation
3 - Borel Sets, Analytic Sets and Beyond: Δ21
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp 51-70
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp i-iv
-
- Chapter
- Export citation
4 - Infinite Combinatorics in Rn: Shift-Compactness
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp 71-77
-
- Chapter
- Export citation
References
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp 291-323
-
- Chapter
- Export citation
5 - Kingman Combinatorics and Shift-Compactness
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp 78-85
-
- Chapter
- Export citation