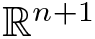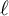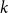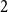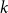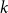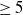Refine search
Actions for selected content:
25814 results in Abstract analysis
Mean values of multiplicative functions and applications to residue-class distribution
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 712-730
-
- Article
- Export citation
JMJ volume 24 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. f1-f2
- Print publication:
- March 2025
-
- Article
-
- You have access
- Export citation
Anisotropic weighted isoperimetric inequalities for star-shaped and F-mean convex hypersurface
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-17
-
- Article
- Export citation
RANK 2
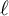 $\ell $-ADIC LOCAL SYSTEMS AND HIGGS BUNDLES OVER A CURVE
$\ell $-ADIC LOCAL SYSTEMS AND HIGGS BUNDLES OVER A CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 891-960
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JMJ volume 24 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. b1-b2
- Print publication:
- March 2025
-
- Article
-
- You have access
- Export citation
Face enumeration for split matroid polytopes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 07 February 2025, pp. 528-544
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The rigidity of filtered colimits of n-cluster tilting subcategories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-14
-
- Article
- Export citation
Extending Wormald’s differential equation method to one-sided bounds
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 06 February 2025, pp. 545-558
-
- Article
- Export citation
On the L-polynomials of curves over finite fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Satisfiability thresholds for regular occupation problems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 04 February 2025, pp. 491-527
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Critical configurations of the hard-core model on square grid graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 04 February 2025, pp. 445-485
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on separability in outer automorphism groups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 04 February 2025, pp. 705-711
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the structure of non-negative integer sets which have identical representation functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 655-674
-
- Article
- Export citation
Right-angled Artin groups and the cohomology basis graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 634-654
-
- Article
- Export citation
Schwarz lemma for harmonic functions in the unit ball
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 616-633
-
- Article
- Export citation
Noetherianity of twisted Zhu’s algebras and bimodules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 675-704
-
- Article
- Export citation

Functional Analysis
-
- Published online:
- 31 January 2025
- Print publication:
- 21 September 2023
-
- Textbook
- Export citation
Local delta invariants of weak del Pezzo surfaces with the anti-canonical degree
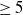 $\geq 5$
$\geq 5$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 269-306
- Print publication:
- May 2025
-
- Article
- Export citation
Large deviation principle for slow-fast rough differential equations via controlled rough paths
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 January 2025, pp. 1-31
-
- Article
- Export citation
Exponential turnpike property for particle systems and mean-field limit
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 993-1011
-
- Article
-
- You have access
- Open access
- HTML
- Export citation