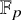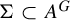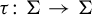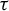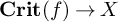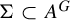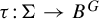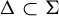Refine listing
Actions for selected content:
73 results in 14Axx
BEAUVILLE–LASZLO GLUING OF ALGEBRAIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 21 January 2026, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pseudolimits for tangent categories with applications to equivariant algebraic and differential geometry
- Part of
-
- Journal:
- Mathematical Structures in Computer Science / Volume 35 / 2025
- Published online by Cambridge University Press:
- 27 November 2025, e33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GAGA FOR HENSELIAN SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1547-1589
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENDING TORSORS UNDER QUASI-FINITE FLAT GROUP SCHEMES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 45-54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirac geometry II: coherent cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 February 2024, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant sets and nilpotency of endomorphisms of algebraic sofic shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 2859-2900
- Print publication:
- October 2024
-
- Article
- Export citation
Some examples of noncommutative projective Calabi–Yau schemes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 706-726
- Print publication:
- September 2024
-
- Article
- Export citation
Calabi–Yau structures on (quasi-)bisymplectic algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 September 2023, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Balmer spectrum of certain Deligne–Mumford stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 24 May 2023, pp. 1314-1346
- Print publication:
- June 2023
-
- Article
- Export citation
Mapping stacks and categorical notions of properness
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. 530-589
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Rouquier dimension of wrapped Fukaya categories and a conjecture of Orlov
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 01 March 2023, pp. 437-487
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Riemann–Roch for stacky matrix factorizations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 06 December 2022, e108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted algebras of geometric algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 715-730
- Print publication:
- September 2023
-
- Article
- Export citation
Euler continuants in noncommutative quasi-Poisson geometry
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A DERIVED LAGRANGIAN FIBRATION ON THE DERIVED CRITICAL LOCUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 August 2022, pp. 311-345
- Print publication:
- January 2024
-
- Article
- Export citation
On images of subshifts under embeddings of symbolic varieties
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 3131-3149
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mirror symmetry and automorphisms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 July 2022, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New examples of non-Fourier–Mukai functors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 12 August 2022, pp. 1254-1267
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TAMARKIN–TSYGAN CALCULUS AND CHIRAL POISSON COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 751-765
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The integral Hodge conjecture for two-dimensional Calabi–Yau categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 12 April 2022, pp. 287-333
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation