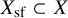Refine listing
Actions for selected content:
240 results in 14Dxx
MODULI SPACES OF SLOPE-SEMISTABLE SHEAVES WITH REFLEXIVE SESHADRI GRADUATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 August 2025, pp. 1-19
-
- Article
- Export citation
Minimal Kinematics on
 $\mathcal{M}_{0,n}$
$\mathcal{M}_{0,n}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moduli spaces of rational graphically stable curves
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 04 August 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEGENERATIONS OF ORBIFOLD CURVES AS NONCOMMUTATIVE VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 15 July 2025, pp. 1-19
-
- Article
- Export citation
Consistent dimer models on surfaces with boundary
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vanishing of Brauer groups of moduli stacks of stable curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e115
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moduli spaces of framed logarithmic and parabolic connections on a Riemann surface
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Upper bounds on the genus of hyperelliptic Albanese fibrations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 02 May 2025, e84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behaviour of large-scale solutions of Hitchin’s equations in higher rank
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kappa classes on KSBA spaces
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A virtual
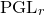 ${\rm PGL}_r$–
${\rm PGL}_r$–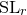 ${\rm SL}_r$ correspondence for projective surfaces
${\rm SL}_r$ correspondence for projective surfaces
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum: Conformal blocks for Galois covers of algebraic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 15 August 2025, pp. 945-946
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
Vector fields and admissible embeddings for quiver moduli
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rationality and arithmetic of the moduli of abelian varieties
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPACT MODULI OF ENRIQUES SURFACES OF DEGREE 2
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 26 February 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EIGENPERIODS AND THE MODULI OF POINTS IN THE LINE
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-24
-
- Article
- Export citation
Smoothing, scattering and a conjecture of Fukaya
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-LOG LIFTABLE LOG DEL PEZZO SURFACES OF RANK ONE IN CHARACTERISTIC FIVE
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-24
-
- Article
- Export citation
Geometrization of the Satake transform for mod p Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 February 2025, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformations of morphisms of sheaves
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 February 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation


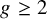
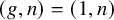
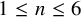
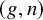
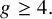




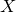
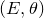
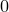
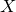
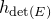
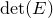
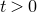
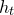
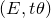
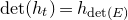
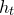
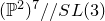
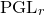
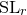
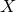
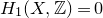
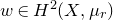
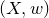
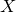
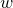
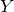
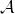
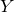
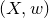
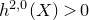
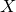
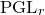
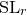
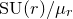
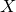
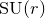
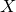
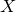
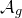
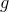
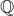
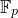
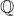
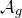
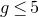
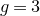
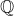

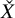
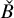
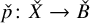
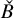
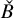
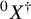 introduced in [8]. Then a comparison between this tropicalized algebra with the dgBV algebra associated to the deformation theory of the semiflat part
introduced in [8]. Then a comparison between this tropicalized algebra with the dgBV algebra associated to the deformation theory of the semiflat part