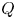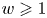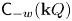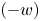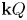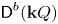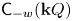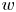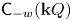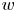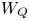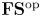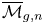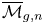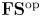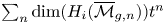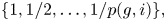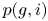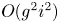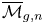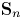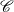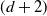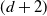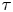Refine listing
Actions for selected content:
149 results in 16Gxx
The generalized auslander–reiten duality on a module category
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 167-181
-
- Article
- Export citation
Functorially finite hearts, simple-minded systems in negative cluster categories, and noncrossing partitions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 23 February 2022, pp. 211-243
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability in the homology of Deligne–Mumford compactifications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 17 December 2021, pp. 2635-2656
- Print publication:
- December 2021
-
- Article
- Export citation
Higher-dimensional Auslander–Reiten theory on (d+2)-angulated categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 October 2021, pp. 527-547
- Print publication:
- September 2022
-
- Article
- Export citation
Unitary representations of type B rational Cherednik algebras and crystal combinatorics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 140-169
- Print publication:
- February 2023
-
- Article
- Export citation
Characterizations of right rejective chains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 July 2021, pp. 557-570
- Print publication:
- September 2022
-
- Article
- Export citation
REPRESENTATION VARIETIES OF ALGEBRAS WITH NODES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 2215-2245
- Print publication:
- November 2022
-
- Article
- Export citation
Report on the finiteness of silting objects
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 07 May 2021, pp. 217-233
-
- Article
- Export citation
Representability and autoequivalence groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 08 February 2021, pp. 657-668
- Print publication:
- November 2021
-
- Article
- Export citation
The symplectic geometry of higher Auslander algebras: Symmetric products of disks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 February 2021, e10
-
- Article
-
- You have access
- Open access
- Export citation
GORENSTEIN SILTING COMPLEXES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 January 2021, pp. 122-135
- Print publication:
- January 2022
-
- Article
- Export citation
Fano quiver moduli
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 December 2020, pp. 984-1000
- Print publication:
- December 2021
-
- Article
- Export citation
SPECIAL TILTING MODULES FOR ALGEBRAS WITH POSITIVE DOMINANT DIMENSION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 09 December 2020, pp. 79-105
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Higher preprojective algebras, Koszul algebras, and superpotentials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 01 February 2021, pp. 2588-2627
- Print publication:
- December 2020
-
- Article
- Export citation
Tropical geometry and Newton–Okounkov cones for Grassmannian of planes from compactifications
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 October 2020, pp. 199-231
- Print publication:
- February 2022
-
- Article
- Export citation
A GENERALIZATION OF THE THEORY OF STANDARDLY STRATIFIED ALGEBRAS I: STANDARDLY STRATIFIED RINGOIDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 07 October 2020, pp. 1-36
- Print publication:
- January 2022
-
- Article
- Export citation
D3-MODULES VERSUS D4-MODULES – APPLICATIONS TO QUIVERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 06 October 2020, pp. 697-723
- Print publication:
- September 2021
-
- Article
- Export citation
Instanton sheaves and representations of quivers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 984-1004
-
- Article
- Export citation
THE COMBINATORICS OF TENSOR PRODUCTS OF HIGHER AUSLANDER ALGEBRAS OF TYPE A
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 29 July 2020, pp. 526-546
- Print publication:
- September 2021
-
- Article
- Export citation
τ-Tilting finite cluster-tilted algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 950-955
-
- Article
- Export citation