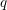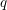Refine listing
Actions for selected content:
149 results in 16Gxx
ASYMPTOTIC TRIANGULATIONS AND COXETER TRANSFORMATIONS OF THE ANNULUS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 27 February 2017, pp. 63-96
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
ON COMPONENTS OF STABLE AUSLANDER–REITEN QUIVERS THAT CONTAIN HELLER LATTICES: THE CASE OF TRUNCATED POLYNOMIAL RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 72-113
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
THE GRADED CENTER OF A TRIANGULATED CATEGORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 74-95
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
EXT-FINITE MODULES FOR WEAKLY SYMMETRIC ALGEBRAS WITH RADICAL CUBE ZERO
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 108-121
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
NEARLY MORITA EQUIVALENCES AND RIGID OBJECTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 225 / March 2017
- Published online by Cambridge University Press:
- 19 August 2016, pp. 64-99
- Print publication:
- March 2017
-
- Article
-
- You have access
- HTML
- Export citation
COHOMOLOGICAL LENGTH FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 223 / Issue 1 / September 2016
- Published online by Cambridge University Press:
- 18 August 2016, pp. 136-161
- Print publication:
- September 2016
-
- Article
-
- You have access
- HTML
- Export citation
Quivers with loops and generalized crystals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 1999-2040
- Print publication:
- October 2016
-
- Article
- Export citation
Mirković–Vilonen polytopes and Khovanov–Lauda–Rouquier algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 1648-1696
- Print publication:
- August 2016
-
- Article
- Export citation
DISTRIBUTIVE LATTICES OF TILTING MODULES AND SUPPORT τ-TILTING MODULES OVER PATH ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 503-511
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
PROGRESS ON THE AUSLANDER–REITEN CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 433-440
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
On the equations and classification of toric quiver varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 265-295
- Print publication:
- April 2016
-
- Article
- Export citation
THE DIMENSION OF A SUBCATEGORY OF MODULES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 09 October 2015, e19
-
- Article
-
- You have access
- Open access
- Export citation
Quantum groups via cyclic quiver varieties I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 299-326
- Print publication:
- February 2016
-
- Article
- Export citation
TILTED ALGEBRAS AND CROSSED PRODUCTS*
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 559-571
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
ON SEMIGENERIC TAMENESS AND BASE FIELD EXTENSION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 39-53
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
The Green Rings of Minimal Hopf Quivers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 11 June 2015, pp. 107-141
-
- Article
- Export citation
Generalized friezes and a modified Caldero–Chapoton map depending on a rigid object
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 101-124
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Champ: a Cherednik algebra Magma package
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 266-307
-
- Article
-
- You have access
- Export citation
Block–Göttsche invariants from wall-crossing
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 8 / August 2015
- Published online by Cambridge University Press:
- 12 March 2015, pp. 1543-1567
- Print publication:
- August 2015
-
- Article
- Export citation
FINITISTIC DIMENSIONS AND PIECEWISE HEREDITARY PROPERTY OF SKEW GROUP ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 509-517
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
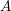
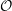
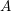
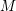
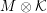
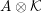
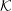
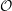
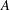
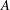
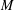
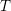
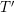
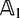
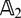
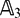
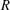
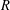
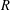
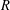
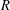
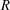
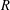
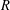
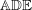
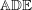
 be a field and let
be a field and let 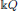 . Tensor categories of the form rep
. Tensor categories of the form rep