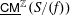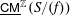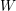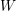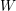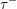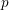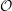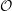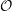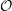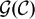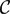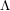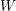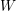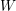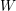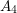Refine listing
Actions for selected content:
149 results in 16Gxx
ON COMPONENTS OF STABLE AUSLANDER–REITEN QUIVERS THAT CONTAIN HELLER LATTICES: THE CASE OF TRUNCATED POLYNOMIAL RINGS – CORRIGENDUM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 14 January 2019, pp. 211-216
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
ANALOGUES OF CENTRALIZER SUBALGEBRAS FOR FIAT 2-CATEGORIES AND THEIR 2-REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1793-1829
- Print publication:
- November 2020
-
- Article
- Export citation
On Knörrer Periodicity for Quadric Hypersurfaces in Skew Projective Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 896-911
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Almost Gentle Algebras and their Trivial Extensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 489-504
-
- Article
- Export citation
Fields of Definition for Representations of Associative Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 November 2018, pp. 291-304
-
- Article
- Export citation
The Gorenstein-projective modules over a monomial algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 02 October 2018, pp. 1115-1134
- Print publication:
- December 2018
-
- Article
- Export citation
DIFFERENTIAL GRADED ENDOMORPHISM ALGEBRAS, COHOMOLOGY RINGS AND DERIVED EQUIVALENCES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 12 September 2018, pp. 557-573
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
The Projective Leavitt Complex
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 1155-1177
-
- Article
- Export citation
Lattice structure of Weyl groups via representation theory of preprojective algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1269-1305
- Print publication:
- June 2018
-
- Article
- Export citation
GRASSMANNIAN SEMIGROUPS AND THEIR REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 27 March 2018, pp. 308-337
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
STRONGLY QUASI-HEREDITARY ALGEBRAS AND REJECTIVE SUBCATEGORIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 27 February 2018, pp. 10-38
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
Integrable Derivations and Stable Equivalences of Morita Type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 343-362
-
- Article
- Export citation
SIMPLE MODULES IN THE AUSLANDER–REITEN QUIVER OF PRINCIPAL BLOCKS WITH ABELIAN DEFECT GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 05 February 2018, pp. 58-85
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
ROUQUIER’S CONJECTURE AND DIAGRAMMATIC ALGEBRA
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 16 November 2017, e27
-
- Article
-
- You have access
- Open access
- Export citation
A CRITERION FOR THE JACOBSON SEMISIMPLICITY OF THE GREEN RING OF A FINITE TENSOR CATEGORY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 25 September 2017, pp. 253-272
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
On categories
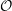 ${\mathcal{O}}$ for quantized symplectic resolutions
${\mathcal{O}}$ for quantized symplectic resolutions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 2445-2481
- Print publication:
- December 2017
-
- Article
- Export citation
Cluster categories for marked surfaces: punctured case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 15 June 2017, pp. 1779-1819
- Print publication:
- September 2017
-
- Article
- Export citation
LATTICE STRUCTURE OF TORSION CLASSES FOR HEREDITARY ARTIN ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 05 June 2017, pp. 89-100
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
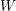 $W$ -GRAPHS AND GYOJA’S
$W$ -GRAPHS AND GYOJA’S 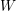 $W$ -GRAPH ALGEBRA
$W$ -GRAPH ALGEBRA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 226 / June 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1-43
- Print publication:
- June 2017
-
- Article
-
- You have access
- HTML
- Export citation
Homomorphisms between standard modules over finite-type KLR algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 621-646
- Print publication:
- March 2017
-
- Article
- Export citation